Domino Dancing

Dois dos meus hobbies prediletos são resolver puzzles e desafios de programação. Por isso, é natural que eu me empolgue quando consigo fazer os dois ao mesmo tempo!

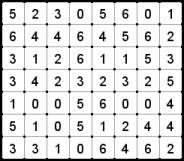
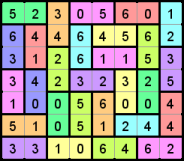
O caso em questão é o problema DOMINO do spojinho. O problema pede pra você resolver computacionalmente um puzzle clássico, que consiste de um tabuleiro 7x8 com números em cada casa, que deve ser completamente preenchido pelos 28 dominós. Esse puzzle é comum em coletâneas como a Denksel da Croco-Puzzle, e também tem disponível online em vários sites, como a applet java do Janko. Abaixo, um exemplo de puzzle no estado inicial e resolvido:


Como resolver computacionalmente esse puzzle? Quem tem alguma experiência logo nota que dá pra resolver com backtracking. Quem tem muita experiência, percebe que, na verdade, esse problema é uma instância do Exact Cover!

De fato, pra modelar o puzzle como um exact cover, basta verificar os constraints: você precisa colocar cada um dos 28 dominós no tabuleiro, e cada uma das 56 casas do tabuleiro deve estar ocupada por um único dominó. Assim, a matriz terá 84 colunas.

As linhas você obtém notando que cada bloco 2x1 ou 1x2 do tabuleiro só pode ser preenchido por um único dominó. Daí, você tem 49 jeitos diferentes de encaixar um dominó na horizontal, e 48 jeitos de encaixar na vertical, então o total de linhas será 97.

Com a matriz 97x84 em mãos o problema está praticamente resolvido, basta implementar um algoritmo de exact cover. As vantagens dessa abordagem são três: primeiro, reduzir a um problema mais genérico é elegante, segundo, você pode reusar código de algum outro exact cover que você já tenha feito na vida. Por fim, como o exact cover é um problema bem conhecido, é de se esperar que a literatura tenha soluções espertas para esse algoritmo, e há mesmo: o exact cover pode ser resolvido com um algoritmo popularizado pelo Knuth, os Dancing Links.


O exact cover em si é NP-Completo, e a solução naïve é exponencial. Usando Dancing Links, você pode implementar uma heurística muito rápida, que diminui consideravelmente o branching factor da busca pela solução. Quem quiser entender a fundo o algoritmo, só precisa ler o paper original do Knuth, a minha implementação em C++ é a abaixo:

Dancing Links em C++

(Warning: Se você tem dificuldade com listas ligadas e medo de listas circulares biligadas, passe longe do Dancing Links. A implementação requer uma lista bicircular pentaligada, o que pode causar graves coceiras em quem tem alergia a ponteiros).

O exact cover também pode ser usado pra resolver o Sudoku e o N-Queens, então é uma técnica que vale a pena conhecer.