Variações sobre um tema

Pelos idos de 2006, um dos meus hobbies era resolver Sudokus. Como eu sou uma criatura que se empolga fácil, tinha sudokus em papel, jogos de sudoku no Nintendo DS, sudokus em tudo quanto é lugar. Depois de algum tempo eu tive que desistir dos sudokus, mas não foi porque eu enjoei, foi porque eu não achava mais puzzles no meu nível!

Os puzzles da Coquetel, por exemplo, podem ser resolvidos quase que exclusivamente com técnicas simples, e esses eu resolvia em poucos minutos. Só os puzzles marcados como "diabólicos" e "grande mestre" que precisavam de alguma técnica mais avançada, como X-Wing e unicidade de soluções.

Mas ainda assim eu não parei de comprar as revistinhas. O Hofstadter dizia, no Metamagical Themas, que "Making variations on a theme is really the crux of creativity", e o povo dos sudokus levou isso a sério. Os sudokus tradicionais já não tinham mais graça, mas a Coquetel também publica variações sobre o tema, como os Sudokus Irregulares:


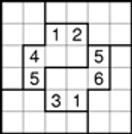
Nesse irregular 6x6 valem as mesmas regras dos sudokus normais, cada linha, coluna ou região precisa ter todos os números de 1 a 6. Mas a maioria das técnicas avançadas não funciona, então esses puzzles ainda têm graça pra mim.

Computacionalmente, o sudoku irregular também pode ser resolvido com o exact cover. No caso desse irregular 6x6, a matriz resultante tem 216x144 elementos. Como eu já tinha a biblioteca de dancing links do post anterior, criar um solver para esse sudoku foi bem simples:

Solver do sudoku irregular 6x6
Entrada exemplo para o solver
Update da lib de exact cover

Dessa vez eu mudei um pouco a api do exactcover.h, a versão original só permitia contar o número de soluções possíveis, agora ela é um template que recebe um functor que é chamado a cada solução encontrada. Como o template ficou mais genérico, agora você pode implementar a variação que quiser sobre o processamento das soluções :)