Potências ótimas
Olhando no Google Analytics, eu descobri que alguém chegou aqui no blog procurando por "como implementar em c++ potências". Se você é essa pessoa, a resposta está abaixo. Se você não é essa pessoa, puxe uma cadeira que o papo é divertido :)
Calcular potências aproximadas em ponto flutuante é trivial, basta incluir a biblioteca <cmath> e usar a função pow, que internamente é implementada como exp(y*log(x)). Mas existem várias aplicações onde você precisa do valor exato da potência, como, por exemplo, durante a criptografia RSA. Nesses casos, uma primeira abordagem pode ser como no código abaixo:
int natural(int x, int n) {
int result = 1;
for (int i = 1; i <= n; i++)
result *= x;
return result;
}
 Esse código funciona, mas existem maneiras mais espertas. Nós, que temos dez dedos, não estamos acostumados a pensar em binário. Mas se fôssemos como os golfinhos, que tem um cérebro maior que o nosso e só duas barbatanas, poderíamos visualizar o expoente em binário e fazer um código assim:
Esse código funciona, mas existem maneiras mais espertas. Nós, que temos dez dedos, não estamos acostumados a pensar em binário. Mas se fôssemos como os golfinhos, que tem um cérebro maior que o nosso e só duas barbatanas, poderíamos visualizar o expoente em binário e fazer um código assim:
int binary(int x, int n) {
if (n == 0) return 1;
if (n == 1) return x;
int half = binary(x, n/2);
if (n & 1)
return half*half*x;
else
return half*half;
}
A versão original era O(n), essa é O(log n), uma melhoria significativa. Mas a melhor notícia sobre esse algoritmo é que você não precisa implementá-lo, ele já está pronto na biblioteca padrão do C++. Basta incluir <ext/numeric> e usar a função power. A função da STL ainda recebe como argumento opcional um functor de multiplicação, então você pode implementar com ela exponenciação modular, ou até mesmo potências de matrizes (ela funciona mesmo que sua multiplicação não seja comutativa).
Por outro lado, esse algoritmo é prático, mas não é ótimo. Em alguns casos, existem maneiras mais rápidas de calcular a potência, o primeiro caso onde isso acontece é para n15. O algoritmo binário precisa de seis multiplicações para resolver o problema, mas existem soluções com apenas cinco:
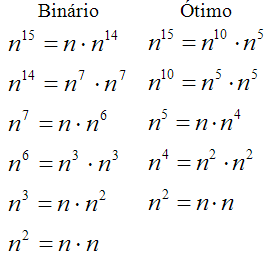
A melhor maneira de descrever as multiplicações necessárias para calcular uma potência é através de uma addition chain. Uma addition chain é uma espécie de generalização da seqüência de Fibonacci: enquanto no Fibonacci o próximo elemento é a soma dos dois imediatamente precedentes, numa addition chain o próximo elemento é a soma de dois anteriores quaisquer, ou até mesmo a soma de um elemento anterior com ele mesmo (com a restrição de que a seqüência precisa ser estritamente crescente).
Pela regra de formação dá pra perceber que, ao contrário da seqüência de Fibonacci, existem inúmeras addition chains. E melhor ainda, você pode associar uma addition chain com a seqüência de expoentes gerados no cálculo de uma potência. Para o exemplo de n=15 acima, as duas addition chains correspondentes são [1 2 3 6 7 14 15] e [1 2 4 5 10 15].
 Achar uma seqüência ótima para calcular potências, então, é equivalente a achar uma addition chain de tamanho mínimo terminada no número que queremos. Infelizmente, eu tenho duas más notícias: o Erdös mostrou que a addition chain ótima não cresce mais lentamente que O(log n), então assintoticamente ela não é melhor que o método binário; e pior, o cálculo da addition chain ótima é NP-Completo. Abaixo eu implementei a addition chain ótima em C++ (usando brute force, então está bem lento):
Achar uma seqüência ótima para calcular potências, então, é equivalente a achar uma addition chain de tamanho mínimo terminada no número que queremos. Infelizmente, eu tenho duas más notícias: o Erdös mostrou que a addition chain ótima não cresce mais lentamente que O(log n), então assintoticamente ela não é melhor que o método binário; e pior, o cálculo da addition chain ótima é NP-Completo. Abaixo eu implementei a addition chain ótima em C++ (usando brute force, então está bem lento):
Implementação da addition chain ótima em C++
É interessante também dar uma olhada nos casos onde o binário perde. No gráfico abaixo, a linha vermelha é o método binário, a linha azul é a addition chain ótima, e a linha verde é log2n:
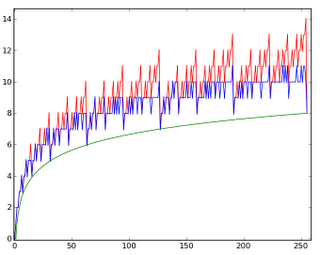
Olhando o gráfico, um golfinho certamente perceberia que o desvio do método binário é proporcional à quantidade de dígitos 1 na representação binária do expoente (os picos são em 63, 127, 255, e assim por diante). A demonstração disso é bem simples e está no Seminumerical Algorithms, junto com várias heurísticas para aproximar a addition chain ótima.

Calcular potências aproximadas em ponto flutuante é trivial, basta incluir a biblioteca <cmath> e usar a função pow, que internamente é implementada como exp(y*log(x)). Mas existem várias aplicações onde você precisa do valor exato da potência, como, por exemplo, durante a criptografia RSA. Nesses casos, uma primeira abordagem pode ser como no código abaixo:
int natural(int x, int n) {
int result = 1;
for (int i = 1; i <= n; i++)
result *= x;
return result;
}
 Esse código funciona, mas existem maneiras mais espertas. Nós, que temos dez dedos, não estamos acostumados a pensar em binário. Mas se fôssemos como os golfinhos, que tem um cérebro maior que o nosso e só duas barbatanas, poderíamos visualizar o expoente em binário e fazer um código assim:
Esse código funciona, mas existem maneiras mais espertas. Nós, que temos dez dedos, não estamos acostumados a pensar em binário. Mas se fôssemos como os golfinhos, que tem um cérebro maior que o nosso e só duas barbatanas, poderíamos visualizar o expoente em binário e fazer um código assim:int binary(int x, int n) {
if (n == 0) return 1;
if (n == 1) return x;
int half = binary(x, n/2);
if (n & 1)
return half*half*x;
else
return half*half;
}
A versão original era O(n), essa é O(log n), uma melhoria significativa. Mas a melhor notícia sobre esse algoritmo é que você não precisa implementá-lo, ele já está pronto na biblioteca padrão do C++. Basta incluir <ext/numeric> e usar a função power. A função da STL ainda recebe como argumento opcional um functor de multiplicação, então você pode implementar com ela exponenciação modular, ou até mesmo potências de matrizes (ela funciona mesmo que sua multiplicação não seja comutativa).
Por outro lado, esse algoritmo é prático, mas não é ótimo. Em alguns casos, existem maneiras mais rápidas de calcular a potência, o primeiro caso onde isso acontece é para n15. O algoritmo binário precisa de seis multiplicações para resolver o problema, mas existem soluções com apenas cinco:
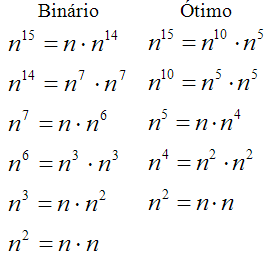
A melhor maneira de descrever as multiplicações necessárias para calcular uma potência é através de uma addition chain. Uma addition chain é uma espécie de generalização da seqüência de Fibonacci: enquanto no Fibonacci o próximo elemento é a soma dos dois imediatamente precedentes, numa addition chain o próximo elemento é a soma de dois anteriores quaisquer, ou até mesmo a soma de um elemento anterior com ele mesmo (com a restrição de que a seqüência precisa ser estritamente crescente).
Pela regra de formação dá pra perceber que, ao contrário da seqüência de Fibonacci, existem inúmeras addition chains. E melhor ainda, você pode associar uma addition chain com a seqüência de expoentes gerados no cálculo de uma potência. Para o exemplo de n=15 acima, as duas addition chains correspondentes são [1 2 3 6 7 14 15] e [1 2 4 5 10 15].
 Achar uma seqüência ótima para calcular potências, então, é equivalente a achar uma addition chain de tamanho mínimo terminada no número que queremos. Infelizmente, eu tenho duas más notícias: o Erdös mostrou que a addition chain ótima não cresce mais lentamente que O(log n), então assintoticamente ela não é melhor que o método binário; e pior, o cálculo da addition chain ótima é NP-Completo. Abaixo eu implementei a addition chain ótima em C++ (usando brute force, então está bem lento):
Achar uma seqüência ótima para calcular potências, então, é equivalente a achar uma addition chain de tamanho mínimo terminada no número que queremos. Infelizmente, eu tenho duas más notícias: o Erdös mostrou que a addition chain ótima não cresce mais lentamente que O(log n), então assintoticamente ela não é melhor que o método binário; e pior, o cálculo da addition chain ótima é NP-Completo. Abaixo eu implementei a addition chain ótima em C++ (usando brute force, então está bem lento):Implementação da addition chain ótima em C++
É interessante também dar uma olhada nos casos onde o binário perde. No gráfico abaixo, a linha vermelha é o método binário, a linha azul é a addition chain ótima, e a linha verde é log2n:

Olhando o gráfico, um golfinho certamente perceberia que o desvio do método binário é proporcional à quantidade de dígitos 1 na representação binária do expoente (os picos são em 63, 127, 255, e assim por diante). A demonstração disso é bem simples e está no Seminumerical Algorithms, junto com várias heurísticas para aproximar a addition chain ótima.
Marcadores: binário, code, complexidade, cpp, criptologia, math

3 Comentários:
Hum... essa caixa de cereal só faltava anunciar "with tasty fun bits!", ou quem sabe "with vitamin RICh BITS"! argh! hahaha acho melhor eu ir dormir, vou contar carneirinhos em potências binárias... :D
Por Al Scandar, Às
28 de maio de 2008 23:10
Al Scandar, Às
28 de maio de 2008 23:10
Ou, como diriam os golfinhos, "so long and thanks for all the fishes !".
Por J Kögler, Às
29 de maio de 2008 20:36
J Kögler, Às
29 de maio de 2008 20:36
Gostei muito do artigo!
Parabéns! Divulgado no Kodumaro. ;-)
[]'s
Cacilhas, La Batalema
Por La Batalema Pitonisto, Às
2 de junho de 2008 21:44
La Batalema Pitonisto, Às
2 de junho de 2008 21:44
Postar um comentário
Links para esta postagem:
Criar um link
<< Início