Aproximações
Ao longo da vida, encontramos aproximações a todo momento. Na escola, a gravidade é aproximadamente 10 m/s2, e a velocidade da luz é aproximadamente 3x108 m/s. Segundo a Bíblia, pi é aproximadamente três (1 Reis 7:23). Mas a minha aproximação predileta é uma que os computeiros usam a todo momento: infinito é aproximadamente oito!
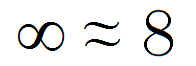 De fato, essa aproximação é o que permite aos computadores trabalhar com números negativos, através do complemento de dois. Lembrando a regra, para calcular o oposto de um número qualquer, basta inverter os bits e somar um. Vamos ver na prática como isso funciona, calculando o oposto de 5.
De fato, essa aproximação é o que permite aos computadores trabalhar com números negativos, através do complemento de dois. Lembrando a regra, para calcular o oposto de um número qualquer, basta inverter os bits e somar um. Vamos ver na prática como isso funciona, calculando o oposto de 5.
Cinco em binário é 101b, e pode ser escrito também como uma soma de potências de dois: 1+4. Para inverter os bits de 5, precisamos lembrar que há infinitos zeros na frente do 101b, então o inverso vai ter infinitas potências de dois:
Esse valor, y=~x+1, não se parece com -5. Mas as coisas ficam mais claras se você multiplicar y por dois, parcela a parcela, ...
... e depois subtrair esse valor do original:
Todos as parcelas maiores que 16 cancelam, e do lado de cá, 2y menos y é o próprio y. Então y=-5, QED. Quando calculamos complementos de dois no computador, usualmente fazemos as contas apenas em um byte, mas, no fundo, é a mesma coisa: ao invés de fazer a conta com infinitas parcelas, você aproxima o valor por apenas 8 parcelas.
 Seu professor de Cálculo 4 certamente deve ter te avisado dos horrores de manipular seqüências divergentes, que invariavelmente levam a paradoxos (como somar apenas parcelas positivas e obter um resultado negativo). No entanto, às vezes até os paradoxos têm utilidades práticas :)
Seu professor de Cálculo 4 certamente deve ter te avisado dos horrores de manipular seqüências divergentes, que invariavelmente levam a paradoxos (como somar apenas parcelas positivas e obter um resultado negativo). No entanto, às vezes até os paradoxos têm utilidades práticas :)
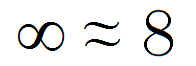 De fato, essa aproximação é o que permite aos computadores trabalhar com números negativos, através do complemento de dois. Lembrando a regra, para calcular o oposto de um número qualquer, basta inverter os bits e somar um. Vamos ver na prática como isso funciona, calculando o oposto de 5.
De fato, essa aproximação é o que permite aos computadores trabalhar com números negativos, através do complemento de dois. Lembrando a regra, para calcular o oposto de um número qualquer, basta inverter os bits e somar um. Vamos ver na prática como isso funciona, calculando o oposto de 5.Cinco em binário é 101b, e pode ser escrito também como uma soma de potências de dois: 1+4. Para inverter os bits de 5, precisamos lembrar que há infinitos zeros na frente do 101b, então o inverso vai ter infinitas potências de dois:
x = 1 + 4
~x = 2 + 8 + 16 + 32 + ...
~x+1 = 1 + 2 + 8 + 16 + 32 + ...
Esse valor, y=~x+1, não se parece com -5. Mas as coisas ficam mais claras se você multiplicar y por dois, parcela a parcela, ...
y = 1 + 2 + 8 + 16 + 32 + ...
2y = 2 + 4 + 16 + 32 + ...
... e depois subtrair esse valor do original:
2y = 2 + 4 + 16 + 32 + ...
y = 1 + 2 + 8 + 16 + 32 + ...
2y-y = -1 + 4 - 8
y = -5
Todos as parcelas maiores que 16 cancelam, e do lado de cá, 2y menos y é o próprio y. Então y=-5, QED. Quando calculamos complementos de dois no computador, usualmente fazemos as contas apenas em um byte, mas, no fundo, é a mesma coisa: ao invés de fazer a conta com infinitas parcelas, você aproxima o valor por apenas 8 parcelas.
 Seu professor de Cálculo 4 certamente deve ter te avisado dos horrores de manipular seqüências divergentes, que invariavelmente levam a paradoxos (como somar apenas parcelas positivas e obter um resultado negativo). No entanto, às vezes até os paradoxos têm utilidades práticas :)
Seu professor de Cálculo 4 certamente deve ter te avisado dos horrores de manipular seqüências divergentes, que invariavelmente levam a paradoxos (como somar apenas parcelas positivas e obter um resultado negativo). No entanto, às vezes até os paradoxos têm utilidades práticas :)

3 Comentários:
Post bacana, eu mesmo nao tinha parado pra pensar no significado do complemento de dois. Sobre a sequencia divergente, eu tenho um comentario: tudo bem que a representacao em serie de ~x e' divergente, mas nao poderiamos montar um mapeamento em que os coeficientes dessa serie seriam aplicados em potencias negativas de 2, ao inves das potencias positivas? Neste caso, sempre teriamos uma sequencia convergente. Portanto, no fundo, nao estamos realmente lidando com uma serie divergentes.
Por Fabio, Às
5 de junho de 2008 14:59
Fabio, Às
5 de junho de 2008 14:59
Se você quiser demonstrar as propriedades do complemento de dois sem usar séries divergentes, o jeito mais fácil é trabalhar no GF(256).
Agora, se você realmente quiser encarar a série infinita sem problemas de divergência, o segredo é usar os p-ádicos.
Por ricbit, Às
6 de junho de 2008 01:09
ricbit, Às
6 de junho de 2008 01:09
Nunca tinha parado para pensar sobre isto.
Enfim, já dei aulas de eletrônica, e ensinei esta matéria. Se eu soubesse disto na época, poderia deixar meus alunos sem dormir.
Por Zephirus, Às
16 de novembro de 2009 12:18
Zephirus, Às
16 de novembro de 2009 12:18
Postar um comentário
Links para esta postagem:
Criar um link
<< Início