Programa de milhagem
Olhando no Google Analytics, eu descobri que alguém chegou aqui no blog procurando por "transformar kilometros em arquivo binarios". Se você é essa pessoa, desculpe, mas eu não entendi sua dúvida. Se você não é essa pessoa, puxe uma cadeira pra ver como até uma pergunta sem sentido pode ser desenvolvida num tema interessante :)
 Uma coisa que me incomoda toda vez que venho pra Califórnia é ter que lidar com milhas e libras. Eu cresci com o sistema métrico: se você me disser que a distância de São Paulo pra Florianópolis é de 700km, eu sei o que isso significa. Agora, se você me disser que a distância de San Francisco pra Mountain View é de 100 milhas, minha intuição falha, e eu vou precisar converter pra km pra poder ter noção da distância.
Uma coisa que me incomoda toda vez que venho pra Califórnia é ter que lidar com milhas e libras. Eu cresci com o sistema métrico: se você me disser que a distância de São Paulo pra Florianópolis é de 700km, eu sei o que isso significa. Agora, se você me disser que a distância de San Francisco pra Mountain View é de 100 milhas, minha intuição falha, e eu vou precisar converter pra km pra poder ter noção da distância.
Como esperado, converter mentalmente de milhas pra km é algo que faço todo o tempo por aqui. Existem várias maneiras de converter de cabeça, mas a filosofia Ricbit dita que, de várias maneiras equivalentes, o correto é escolher a mais bizarra! Sendo assim, vou mostrar a conversão utilizando números de Fibonacci.
 Todo mundo conhece os números de Fibonacci, eles estão em todo lugar. Em minha época de estudante, uma das minhas diversões secretas era entrar escondido no andar superior da biblioteca do IME só pra ler a Fibonacci Quartely. Os leitores assíduos da revista conhecem um monte de fatos curiosos sobre os Fibonacci, e eu vou usar dois deles aqui.
Todo mundo conhece os números de Fibonacci, eles estão em todo lugar. Em minha época de estudante, uma das minhas diversões secretas era entrar escondido no andar superior da biblioteca do IME só pra ler a Fibonacci Quartely. Os leitores assíduos da revista conhecem um monte de fatos curiosos sobre os Fibonacci, e eu vou usar dois deles aqui.
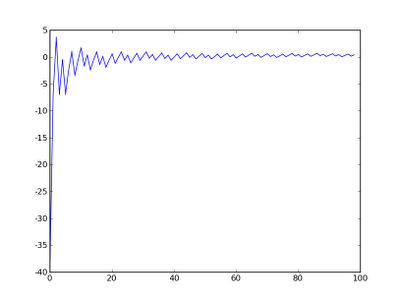
O primeiro é que os números da seqüência de Fibonacci podem ser calculados diretamente, sem precisar fazer toda a recursão F(n+2)=F(n+1)+F(n). Pra isso, basta calcular qual o inteiro mais próximo da expressão abaixo:
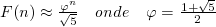
Na expressão acima, o phi é a conhecida razão áurea. A demostração dessa fórmula é elementar e fácil de encontrar na web.
O segundo é que qualquer número pode ser escrito como uma soma de números distintos de Fibonacci. Por exemplo, 100 pode escrito como 89+8+3. Daí, se você enfileirar os números de Fibonacci, e atribuir a cada número 1 se ele é usado na soma, e 0 se não é, você pode atribuir a qualquer inteiro uma string de zeros e uns que funciona como uma espécie de base binária alternativa (o povo chama isso de base de Fibonacci).
Fazendo o processo com o número 100, chegamos em 10000101000. Essa base tem algumas propriedades curiosas, por exemplo, ela não é bijetora (de fato, você pode escrever 100 de outras maneiras, como 1100101000). Uma base numérica que tem representação múltipla tem utilidades bastante curiosas em design de circuitos elétricos (mas isso é uma história pra outro dia :).
Além disso, cada número possui pelo menos uma representação onde não há nenhuma seqüência com dois uns consecutivos (pela própria definição de Fibonacci, se houver dois uns em algum ponto, você pode apagá-los e trocar por um único 1 na posição seguinte). Esse fato é explorado em alguns tipos de sinalização, para fazer detecção de erro: se você receber dois uns seguidos, certamente recebeu um erro.
 Mas qual a relação disso com milhas e quilômetros? É simples, para converter de milhas para km, basta fazer um shift de Fibonacci!
Mas qual a relação disso com milhas e quilômetros? É simples, para converter de milhas para km, basta fazer um shift de Fibonacci!
Uma milha equivale a 1.609344 km. A razão áurea é 1.61803399. Os dois números, apesar de não serem relacionados, são muito parecidos, e esse é o truque que vamos usar pra converter. Na base binária tradicional, um shift para a esquerda é equivalente a multiplicar por dois; na base de Fibonacci, um shift para a esquerda equivale a multiplicar pela razão áurea. Então, se você tiver um valor em milhas na base de Fibonacci, um shift irá transformar o valor para o equivalente em quilômetros.
Vamos conferir: 100 é 10000101000. Com um zero extra no final, fica 100001010000, que é 144+13+5=162. Se, ao invés disso, você converter diretamente, teria 160.9km, ou seja, o método realmente aproxima muito bem a conversão! O gráfico abaixo mostra a porcentagem do erro do método em relação ao ideal, e mais abaixo está o programa que converte a milhagem para quilometragem e gera o gráfico:
 Script que plota o gráfico acima, em python
Script que plota o gráfico acima, em python
Como pode ser visto, o método esquenta bem rápido, pra distâncias superiores a 10 milhas o erro é inferior a 5%, e acima disso praticamente desaparece. Em comparação, o método naive de aproximar por 1.5 (multiplicar de cabeça por 3 e dividir por 2), tem um erro constante de mais ou menos 8%.
 Uma coisa que me incomoda toda vez que venho pra Califórnia é ter que lidar com milhas e libras. Eu cresci com o sistema métrico: se você me disser que a distância de São Paulo pra Florianópolis é de 700km, eu sei o que isso significa. Agora, se você me disser que a distância de San Francisco pra Mountain View é de 100 milhas, minha intuição falha, e eu vou precisar converter pra km pra poder ter noção da distância.
Uma coisa que me incomoda toda vez que venho pra Califórnia é ter que lidar com milhas e libras. Eu cresci com o sistema métrico: se você me disser que a distância de São Paulo pra Florianópolis é de 700km, eu sei o que isso significa. Agora, se você me disser que a distância de San Francisco pra Mountain View é de 100 milhas, minha intuição falha, e eu vou precisar converter pra km pra poder ter noção da distância.Como esperado, converter mentalmente de milhas pra km é algo que faço todo o tempo por aqui. Existem várias maneiras de converter de cabeça, mas a filosofia Ricbit dita que, de várias maneiras equivalentes, o correto é escolher a mais bizarra! Sendo assim, vou mostrar a conversão utilizando números de Fibonacci.
 Todo mundo conhece os números de Fibonacci, eles estão em todo lugar. Em minha época de estudante, uma das minhas diversões secretas era entrar escondido no andar superior da biblioteca do IME só pra ler a Fibonacci Quartely. Os leitores assíduos da revista conhecem um monte de fatos curiosos sobre os Fibonacci, e eu vou usar dois deles aqui.
Todo mundo conhece os números de Fibonacci, eles estão em todo lugar. Em minha época de estudante, uma das minhas diversões secretas era entrar escondido no andar superior da biblioteca do IME só pra ler a Fibonacci Quartely. Os leitores assíduos da revista conhecem um monte de fatos curiosos sobre os Fibonacci, e eu vou usar dois deles aqui.O primeiro é que os números da seqüência de Fibonacci podem ser calculados diretamente, sem precisar fazer toda a recursão F(n+2)=F(n+1)+F(n). Pra isso, basta calcular qual o inteiro mais próximo da expressão abaixo:
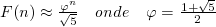
Na expressão acima, o phi é a conhecida razão áurea. A demostração dessa fórmula é elementar e fácil de encontrar na web.
O segundo é que qualquer número pode ser escrito como uma soma de números distintos de Fibonacci. Por exemplo, 100 pode escrito como 89+8+3. Daí, se você enfileirar os números de Fibonacci, e atribuir a cada número 1 se ele é usado na soma, e 0 se não é, você pode atribuir a qualquer inteiro uma string de zeros e uns que funciona como uma espécie de base binária alternativa (o povo chama isso de base de Fibonacci).
Fazendo o processo com o número 100, chegamos em 10000101000. Essa base tem algumas propriedades curiosas, por exemplo, ela não é bijetora (de fato, você pode escrever 100 de outras maneiras, como 1100101000). Uma base numérica que tem representação múltipla tem utilidades bastante curiosas em design de circuitos elétricos (mas isso é uma história pra outro dia :).
Além disso, cada número possui pelo menos uma representação onde não há nenhuma seqüência com dois uns consecutivos (pela própria definição de Fibonacci, se houver dois uns em algum ponto, você pode apagá-los e trocar por um único 1 na posição seguinte). Esse fato é explorado em alguns tipos de sinalização, para fazer detecção de erro: se você receber dois uns seguidos, certamente recebeu um erro.
 Mas qual a relação disso com milhas e quilômetros? É simples, para converter de milhas para km, basta fazer um shift de Fibonacci!
Mas qual a relação disso com milhas e quilômetros? É simples, para converter de milhas para km, basta fazer um shift de Fibonacci!Uma milha equivale a 1.609344 km. A razão áurea é 1.61803399. Os dois números, apesar de não serem relacionados, são muito parecidos, e esse é o truque que vamos usar pra converter. Na base binária tradicional, um shift para a esquerda é equivalente a multiplicar por dois; na base de Fibonacci, um shift para a esquerda equivale a multiplicar pela razão áurea. Então, se você tiver um valor em milhas na base de Fibonacci, um shift irá transformar o valor para o equivalente em quilômetros.
Vamos conferir: 100 é 10000101000. Com um zero extra no final, fica 100001010000, que é 144+13+5=162. Se, ao invés disso, você converter diretamente, teria 160.9km, ou seja, o método realmente aproxima muito bem a conversão! O gráfico abaixo mostra a porcentagem do erro do método em relação ao ideal, e mais abaixo está o programa que converte a milhagem para quilometragem e gera o gráfico:
 Script que plota o gráfico acima, em python
Script que plota o gráfico acima, em pythonComo pode ser visto, o método esquenta bem rápido, pra distâncias superiores a 10 milhas o erro é inferior a 5%, e acima disso praticamente desaparece. Em comparação, o método naive de aproximar por 1.5 (multiplicar de cabeça por 3 e dividir por 2), tem um erro constante de mais ou menos 8%.

13 Comentários:
Você tem tempo demais em suas mãos. :)
Por Bruno, Às
14 de junho de 2008 00:16
Bruno, Às
14 de junho de 2008 00:16
Eu estou na Califórnia, minha namorada e meu wii estão no Brasil :)
Por ricbit, Às
14 de junho de 2008 01:15
ricbit, Às
14 de junho de 2008 01:15
Mais um excelente post! Parabéns!
Por Andrews Medina, Às
14 de junho de 2008 14:26
Andrews Medina, Às
14 de junho de 2008 14:26
Caramba! Pior que funciona...
O que você tomou horas antes de chegar nisso? :-)
Por Cesar, Às
14 de junho de 2008 16:20
Cesar, Às
14 de junho de 2008 16:20
Suco de ramanujan :)
Por ricbit, Às
14 de junho de 2008 21:17
ricbit, Às
14 de junho de 2008 21:17
juro que aparti de agora vou prestar atenção nas aulas.
Por Akihito, Às
15 de junho de 2008 02:05
Akihito, Às
15 de junho de 2008 02:05
The nicest way is translating Pesetas into Euros (the exchange rate is 166.386 pts = 1 €).
We spaniards, have magically learnt how to translate miles into Km. for free. Even not mathematically inclined people.
We also know the x6 multiplication table by heart.
Isaac... (translating miles into km with no fuss since 2002).
Por friguron, Às
16 de junho de 2008 04:09
friguron, Às
16 de junho de 2008 04:09
Amigo, fiquei super impressionado com o nivel do blog, sou um mero programador e pouco atuante no mundo da matemática, entretanto a utilizo em todos os clicks da minha vida. Parabéns!
Percebi que seus meros leitores tem espaço no blog, afinal até conversão de milhagem virou tema. Gostaria de fazer uma pergunta: Como eu resolvo esse problema?
Tenho um valor com 23 casas numéricas ex.: 12345678901234567890123 como eu poderia representar este campo da menor forma possível? Tipo uma redução onde apenas o algorítimo que o reduziu possa entendê-lo e representá-lo novamente. A proposta é deixar o menor possível, pensei em fatoração e exponenciação, porém estou achando muito amador.
Por lucas, Às
9 de julho de 2008 00:33
lucas, Às
9 de julho de 2008 00:33
... enquanto isso, na Batcaverna!
Robin: Eu podia estar matando, eu podia estar roubando, mas estou aqui pedindo uma ajuda! Leia o post acima!
Por lucas, Às
23 de julho de 2008 00:47
lucas, Às
23 de julho de 2008 00:47
Teorema de Shannon né? Você não pode comprimir menos que a entropia da mensagem, e ela é igual a -sum(p[i]*log2(p[i])) onde p[i] é a probabilidade de cada símbolo. Assumindo distribuição uniforme, você tem 10^23 símbolos, a entropia simplifica pra 23*log2(10) que dá uns 75 bits. Esse é o limite teórico, menos que isso só se você usar compressão com perdas.
Por ricbit, Às
23 de julho de 2008 00:56
ricbit, Às
23 de julho de 2008 00:56
Olá Ricardo,
Parabéns pelo post.
Os métodos estatísticos para calcular pi sao fantasticos, nao é mesmo?
Um dia desses mesmo o paliteiro que estava sobre a minha mesa caiu no chao da minha sala, que é feito de tacos de madeira. Lembrei-me de um método estatístico para aproximar pi. Voce o conhece?
Marcelo
Por Marcelo Silva, Às
14 de setembro de 2008 23:10
Marcelo Silva, Às
14 de setembro de 2008 23:10
Sim, sim, dá uma olhada nos comentários do post sobre o pi que tem mais dois métodos lá :)
Por ricbit, Às
14 de setembro de 2008 23:12
ricbit, Às
14 de setembro de 2008 23:12
Caro Ricardo,
Teu blog é realmente muito interessante. Não sou programador (cheguei a iniciar a faculdade de matemática aplicada e computacional, mas logo mudei para a física), mas aprecio muito o conteúdo dos teus posts (sempre ricos em história, matemática, programação, cultura, etc.). Gostei muito da lógica que tu seguiste para montar a tua lista de livros para desenvolvedores e me bateu o maior saudosismo quando li sobre "O Homem que Calculava", que foi o livro que me mostrou o quão incrível e divertida é a matemática (acho que deveria ser leitura obrigatória nas escolas!).
Parabéns!
Por abonatto, Às
17 de setembro de 2008 23:02
abonatto, Às
17 de setembro de 2008 23:02
Postar um comentário
Links para esta postagem:
Criar um link
<< Início