Um cientista em minha vida

Eu li lá no blog do Kentaro que o meme da semana era "Um Cientista em minha vida", onde deveríamos falar sobre algum cientista que fez a diferença pra você. Como eu adoro constrained writing, resolvi participar (na verdade, eu adoro constrained anything, por isso que vivo criando programas em uma linha, programas que rodam em computadores de 8 bits, e assim por diante).

Eu já falo de cientistas aqui todo o tempo. Olhando no histórico, eu já falei do Knuth, do Erdös, do prof. Routo, do prof. Henrique, e de vários outros. Em comum, todos eles foram cientistas que eu conheci depois de adulto. Achei apropriado então que eu falasse de um cientista que fez a diferença quando eu era criança, e pra isso vamos ter que rebobinar até a década de 80.

Se você perguntar pra alguém sobre revistas de computador na década de 80, invariavelmente irá ouvir sobre a Micro Sistemas ("a primeira revista brasileira sobre microcomputadores"). A Micro Sistemas era muito legal, mas o que eu gostava mesmo era de outra revista, menos conhecida, chamada Microhobby.

A diferença da Micro Sistemas pra Microhobby era mais ou menos a diferença de Informática pra Computação. Na primeira, nós ficávamos encantados com as notícias da maravilhosa terra além da reserva de mercado (onde aprendíamos que a Apple planejava lançar um novo computador chamado McIntosh, que vinha com um periférico estranho e esquisito chamado mouse), enquanto que na segunda aprendíamos a calcular geodésicas e a usar o método de Bolzano para achar raízes de uma equação.

Mas o diferencial mesmo da Microhobby eram as colunas escritas pelo Renato da Silva Oliveira. Uma googlada rápida revela que o Renato é formado em Física, trabalhou nos planetários de São Paulo, Campinas, Vitória e Tatuí, e atualmente trabalha em uma empresa que vende planetários infláveis (how cool is that?!). Mas é claro que eu não sabia disso na época, o que eu sabia era que ele contava historinhas!

Foi lendo as historinhas do Renato que eu descobri que era possível escrever sobre ciência e computação, com clareza e bom humor. Pena que isso ainda não é muito difundido, a julgar pela quantidade de crianças que ainda acham que ciência é uma coisa chata :(

As historinhas que ele escrevia sempre tinham o mesmo formato: um certo sr. Nabor Rosenthal, em suas viagens pelo mundo, deparava-se com alguma situação que sugeria uma análise matemática (os tópicos eram os mais variados e iam de teoria dos grafos até contatos com extraterrestres). Depois de ponderar sobre o problema sem conseguir resolvê-lo, o Nabor tomava uma dose do raro Suco de Ramanujan, que o colocava num transe que ampliava suas capacidades analíticas, e conseguia solucionar o problema.

Mas a coluna sempre acabava antes que o Nabor mostrasse qual a solução! Ao invés disso, o leitor tinha um mês pra conseguir resolver o problema, e só no mês seguinte a solução era apresentada. Na década de 80 ainda não tinha spoj, então as colunas do Renato eram o que bombava pra quem gostava de puzzles computacionais.

Um dos puzzles apresentados foi o segundo puzzle mais difícil da minha vida, eu levei mais de dez anos pra conseguir resolver. Em uma das Microhobby, o Nabor entrou em transe após tomar o Suco de Ramanujan, e durante o transe ele sonhou "com um método para calcular o número pi, usando apenas o gerador de números aleatórios de seu micro" (essa era a época onde o micro mais avançado era o TK-82C, com 2kb de RAM).

Na época eu pensei muito e não consegui solucionar, achando que ia precisar de alguma matemática que eu ainda não tinha aprendido. Eu nunca consegui achar a revista seguinte com a solução, tive que passar pelo primário, pelo colégio técnico, e só no meio da faculdade é que caiu a ficha (e eu percebi que poderia ter solucionado ainda no primário, se tivesse insistido o suficiente :)

O truque é o seguinte: você vai fazer N experimentos, cada um consistindo no sorteio de dois números aleatórios escolhidos uniformemente entre 0 e 1. Se soma dos quadrados dos números for menor ou igual a 1, incremente um contador (digamos, M). Ao final dos experimentos, pi=4*M/N. O script abaixo implementa esse algoritmo:

Script em python para calcular pi usando números aleatórios

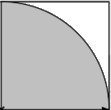O funcionamento é bem simples e baseia-se na figura ao lado. Você começa inscrevendo um quarto de círculo num quadrado de lado 1. Os dois números que você sorteia a cada iteração podem ser interpretados como um ponto dentro do quadrado, e o teste feito é equivalente a testar se o ponto está dentro do círculo ou não. Como a distribuição dos pontos é uniforme, espera-se que a razão M/N seja igual à razão entre as áreas da figura. A área do quadrado é 1, a área do círculo é pi*r². Como o raio é unitário, então a área do quarto de círculo é pi/4. Isolando pi, chega-se em pi=4*M/N, QED.

A pergunta que deve ser feita ao encontrar qualquer algoritmo novo é: qual é sua complexidade? Infelizmente, esse método aleatório é bem ruim. No fundo, o que estamos fazendo é aproximar pi por uma fração, cujo denominador é N. Então a precisão máxima que podemos obter é 1/N, e se você quer calcular n dígitos de pi, esse método converge, no melhor caso, em O(10ⁿ), e na prática em bem menos que isso, porque os seus geradores de números aleatórios não são perfeitamente uniformes.

Eu nunca soube qual o método que o Nabor usou pra calcular o pi. Como ele tinha o Suco de Ramanujan e eu não, espero que tenha sido um método melhor que o meu :)