O algoritmo mais rápido do oeste

Dia desses um amigo me passou um probleminha bem divertido. O enunciado é simples: dado um vetor ordenado, construa uma binary search tree, balanceada, com os mesmos elementos do vetor. Esse problema tem uma solução trivial em O(n log n) e uma solução esperta em O(n), mas eu acabei achando uma terceira solução, com o algoritmo mais rápido do oeste: ele roda em O(0)!

Vamos revisar as respostas tradicionais antes. A solução trivial é usar uma árvore binária auto-balanceante, como a AVL ou a Red-Black, e inserir os elementos nela, um por um. Como você vai inserir n elementos e o custo de inserção é O(log n), então o total desse algoritmo é O(n log n).

Mas fazendo dessa maneira, você não está usando a informação de que o vetor estava ordenado. Com uma recursão simples você consegue aproveitar esse fato, e construir a árvore em apenas O(n). Um exemplo em python é assim:

def build_tree(vector):
  def partition(start, end):
    if (end < start):
      return None
    middle = start + (end-start) / 2
    return (vector[middle], 
            partition(start, middle-1), 
            partition(middle+1, end))
  return partition(0, len(vector) - 1)

Aparentemente, essa solução é ótima. Se você vai criar uma estrutura de dados nova usando os dados da antiga, o mínimo de trabalho que você precisa é copiar os elementos de uma pra outra, e isso limita em O(n) certo? Quase! Você pode contornar essa limitação se usar uma estrutura de dados implícita, e é isso que vamos tentar fazer.

Para usar o vetor ordenado original como uma estrutura implícita, nós precisamos criar um isomorfismo entre o vetor ordenado e a binary search tree. Se for possivel criar esse isomorfismo, então na verdade eu não preciso fazer nada pra converter o vetor, ele já é equivalente à árvore. E um algoritmo que não faz nada é um algoritmo O(0)! Eu poderia chamar essa estrutura de dados nova de Implicit Balanced Binary Search Tree, mas é muito comprido, então vou chamá-la de Cactus Binário (apropriado, daqui em diante as coisas vão ficar espinhosas).

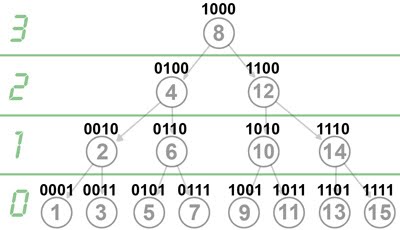
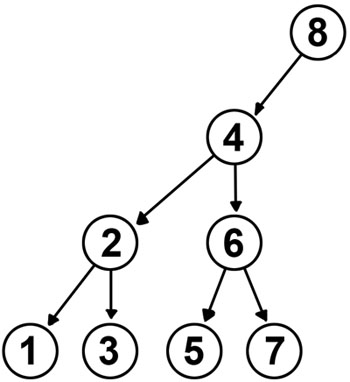
Mas vamos ao isomorfismo então. Como o vetor está ordenado, então os valores dos elementos em si não importam muito, e nós podemos trabalhar só com os índices, sem perda de generalidade. Além disso, para as demonstrações ficarem mais simples, vamos dividir em dois casos. Digamos que o tamanho do vetor é N, então o primeiro caso que vamos tratar é quando N pode ser escrito como 2^h-1 para algum h>0. Nesse caso, o Cactus Binário é uma árvore perfeita (todas as folhas estão no mesmo nível e todos os nós internos tem dois filhos):

Para criar o isomorfismo, eu preciso fornecer duas funções que, para um dado índice, me retornem o índice do filho à esquerda e do filho à direita. Depois de pensar um pouco, acabei chegando nas funções abaixo:

left(x) = x - (x & (-x)) / 2
right(x) = x + (x & (-x)) / 2

Isso é mágica? Não, é matemática! Para entender porque as expressões funcionam, é só olhar para a árvore anterior usando a visão além do alcance:

Olha só que bacana, quando você olha para os índices da árvore em binário, parece que o nível em que está o índice é igual ao número de zeros no final da representação binária dele. Na verdade, nós podemos provar isso, usando indução na altura da árvore.

Vejamos: para uma árvore de altura unitária, o único elemento é o 1, que está no nível zero e tem 0 bits zero no final, então a base de indução está ok. Se a árvore tem altura h, então ela tem 2^h-1 elementos. O elemento central é o 2^h-1, que tem h-1 zeros no final e está no nível h-1. A sub-árvore da esquerda é uma árvore balanceada de tamanho 2^h-1-1, que funciona pela hipótese de indução. A sub-árvore da direita é igual à da esquerda, se você ligar o bit mais significativo de cada índice. Setar o bit mais à esquerda não muda a quantidade de bits zero à direita, então podemos usar a hipótese de indução novamente, e pronto: QED.

Agora ficou fácil achar a fórmula né? Se você tem um índice x no nivel h, então o filho à esquerda é o maior número com h-1 zeros à direita que seja menor que x, e o análogo vale para o filho à direita. Ou seja, pra descer do nível h para o nível h-1 pela esquerda, basta subtrair 2^h-1  (ou somar, se for pela direita).

E computacionalmente como eu faço isso? Basta achar o bit 1 mais à direita do número, dividir isso por dois e subtrair do número original. Para achar o primeiro bit 1, o truque é calcular x & (-x). Vamos provar: pela definição de complemento de dois, negar é o mesmo que inverter e somar um. Se o número em binário for algo do tipo xxxx10000, negado ele fica yyyy01111, e quando você soma um, o carry propaga até bater no zero, ficando yyyy10000. Quando você faz o AND, os primeiros bits dão zero porque o AND de um bit e seu complemento é sempre zero, e os últimos bits dão zero porque o AND de qualquer bit com zero dá zero. Sobra só o primeiro bit 1 à direita, QED.

Juntando tudo agora as duas fórmulas são evidentes. Mas pra completar o isomorfismo eu ainda preciso de uma fórmula que me indique onde está a raiz da árvore. A fórmula em si é simples: a raiz é a maior potência de dois menor ou igual ao tamanho do vetor, ou seja, basta achar o primeiro bit 1 à esquerda do tamanho.

Para achar o primeiro bit 1 à esquerda não tem nenhum truque tão simples quanto à direita, mas felizmente existe uma alternativa: os processadores x86 possuem um opcode meio desconhecido chamado BSR (bit scan reverse), que retorna exatamente onde está esse bit à esquerda. Em processadores bons, como o Core 2 Duo, o BSR é uma operação O(1), mas isso não é verdade em todos os processadores (por exemplo, não é verdade nos AMDs). Se você não tiver o BSR por hardware, pode fazer uma busca binária nos bits do número, que é uma operação O(log log n).

Isso conclui o primeiro caso. Vamos ver agora o que acontece quando o tamanho é um número qualquer. O pior caso do algoritmo é quando o tamanho é uma potência de dois, e o Cactus Binário fica assim:

Uepa! Essa árvore está balanceada? Bem, depende da sua definição de balanceada. Nessa árvore, o maior caminho entre a raiz e uma folha é 4, o que parece muito. Mas, na verdade, não dá criar uma árvore que tenha um caminho máximo menor. Se o caminho máximo fosse 3, então a árvore poderia ter no máximo 7 elementos, e pelo princípio da casa dos pombos a árvore de tamanho 8 com caminho máximo 3 é impossível. De fato, se você tentar balancear mais a árvore, o melhor que você consegue é algo assim:

Logo, o caminho máximo do Cactus Binário é o mesmo caminho máximo da árvore balanceada. Note, entretanto, que isso é melhor que as árvores auto-balanceantes! O caminho máximo da AVL, no pior caso, é 1.44log(n), e o da Red-Black é 2log(n), ambos maiores que o Cactus Binário.

Com isso, nós provamos o isomorfismo para os dois casos, e o algoritmo O(0) realmente funciona! Mas a grande dúvida agora é: ele serve pra alguma coisa? Na verdade, a grande vantagem da árvore binária é que ela faz inserções em O(log n), enquanto que uma inserção no Cactus Binário é apenas O(n). Por isso, nas aplicações práticas da vida real a árvore binária ganha. Aparentemente, a única utilidade do Cactus Binário é para escrever blog posts :)

Mais mágicas com calculadoras

Quando eu era criança, a mágica que eu mais gostava era aquela onde o ilusionista serra a assistente ao meio. Acho que a graça era tentar entender como ele fazia aquilo, levei um tempão para descobrir o truque. Usando uma calculadora também temos um truque parecido, mas ao invés de serrar uma assistente, vamos cortar um número em dois!

Para começar essa mágica, peça para a criança digitar o número mágico 142857 na calculadora:

Agora peça para que ela multiplique esse número por dois:

Olha só! Você cortou o número ao meio e juntou as partes ao contrário, 14-2857 virou 2857-14!

Agora peça para ela digitar novamente o número mágico e multiplicar por três:

Ahá! Novamente você cortou o número ao meio, 1-42857 virou 42857-1.

Você pode continuar a mágica a partir daqui, esse truque funciona com todos os múltiplos até 6:

142857 * 1 = 142857

142857 * 2 = 285714

142857 * 3 = 428571

142857 * 4 = 571428

142857 * 5 = 714285

142857 * 6 = 857142

Aparentemente, a parte díficil desse truque é memorizar o número mágico. Quando você está cercado de crianças barulhentas, não é fácil lembrar 142857! Mas, felizmente, você não precisa decorar o número. É só lembrar que ele é a dizíma periódica de 1/7, e você pode usar a própria calculadora para calcular a dízima:

1/7 = 0.142857142857142857...

A pergunta natural é: tem outras dízimas com essa propriedade, ou o 142857 é especial? Espantosamente, existem sim outros números. Eles tem até nome: são os números cíclicos. Para achar esses outros números, vale a pena entender porque o 1/7 funciona, e para isso é só observar o comportamento da dízima no algoritmo de divisão longa:

Você começa dividindo o número 1, e sempre que o resto é menor que 7, coloca um zero atrás e continua. Note que, quando você divide por 7, só tem sete restos possíveis: 0, 1, 2, 3, 4, 5 e 6. Se o resto for zero em algum momento, a divisão acaba e o resultado é exato. Mas se em algum momento o resto repetir, ou seja, for igual a algum resto que já apareceu antes, então você tem uma dízima.

Os números cíclicos são formados por divisões de período máximo. Como você nunca pode ter um zero de resto, então no caso da dízima de 7, o maior período possível seria seis (felizmente é o caso). Você começa com o resto 1, e quando chega no 1 de novo começa a repetir, como no diagrama abaixo:

Veja como agora dá pra entender porque os números cíclicos funcionam: 142857 é a dízima de 1/7. Se a gente multiplicar 1/7 por dois, teremos 2/7, e a dízima tem que ser o dobro também. Mas se você olhar no diagrama, multiplicar por dois é a mesma coisa que começar a percorrer o diagrama a partir do 2, ao invés de começar no 1. Mas não importa de onde você começa, a seqüência será sempre a mesma, e daí o resultado vai ser uma rotação da dízima original!

Sabendo que os números cíclicos são as dízimas de período máximo, já dá pra começar a procurar propriedades desses números. Quais números, além do 7, geram dízimas de período máximo?

A primeira coisa que a gente nota é que esses números precisam ser primos. O raciocínio é relativamente simples. Vamos chamar esse número que procuramos de k, e fazer a divisão longa de 1 por k. Os restos da divisão longa formam uma recorrência, onde o primeiro termo é 1, e para os seguintes você coloca um zero no final e acha o resto da divisão por k:

R[0] = 1
R[n] = 10*R[n-1] (mod k)

Essa recorrência dá pra resolver de cabeça:

R[n] = 10ⁿ (mod k)

Para termos uma dízima de período máximo, o resto precisa ser 1 novamente quando n=k-1, ou seja:

R[k-1] = 10^k-1 = 1 (mod k)

Agora, do teorema de Euler-Fermat, nós sabemos que:

10^φ(k) = 1 (mod k)

Onde φ(k) é a função totiente. Ora, nós sabemos que, quando k é composto, o totiente é sempre menor que k-1, então k não pode ser composto, e portanto é primo.

Certo, então k precisa ser primo, mas qualquer primo serve? Nope. Tem alguns primos que não funcionam, como por exemplo onze. No caso do 11, é verdade que 10¹⁰ deixa resto 1, mas logo 10² já tem resto 1 também, então a dízima é muito mais curta que gostaríamos.

Na verdade, o segredo desses primos que funcionam é que... hum... ninguém sabe qual o segredo. Esse é um problema em aberto. Na verdade, a coisa é tão feia que ninguém sabe nem mesmo se esses primos são finitos ou infinitos. O melhor que podemos fazer é um script que ache os primeiros deles:

Script em python que acha os primeiros números cíclicos

Depois do sete, o primeiro primo que funciona é o 17, e o número cíclico associado é 0588235294117647. Note que esse é um caso onde o zero à esquerda faz diferença! Se a sua calculadora tiver um visor bem grande, dá pra divertir uma criança por um tempão com esse número :)

Single-Person Pair Programming

Dia desses me perguntaram no twitter o que eu achava de Pair programming. Não apenas eu gosto, como sou entusiasta! Pair programming tem um monte de vantagens, sendo que a principal delas é que o programa será escrito com dois pares de olhos. E como nos lembra a Lei do Beholder Lei de Linus: dados olhos suficientes, todos os bugs são fáceis.

Minha técnica predileta de pair programming é o Ping-Pong Pair Programming, que eu aprendi com o Miško. A idéia é mesclar as idéias do pair programming com o test-driven development. Você começa colocando dois teclados no computador, aí um parceiro escreve um teste, e o outro escreve o código que faz aquele teste passar. A vantagem desse método é que funciona mesmo se um dos programadores for preguiçoso, e, de fato, funciona até melhor assim!

Por exemplo, vamos supor que Alice e Bob querem escrever um programa bem simples: uma função que incrementa um número. Digamos que a assinatura dessa função será int increment(int value). Alice escreve um teste que valida essa função:

void teste1() {
  assertEquals(2, increment(1));
}

Um teste bem razoável. Se entrar um, tem que sair dois. Agora Bob vai escrever o código que faz esse teste passar:

int increment(int value) {
  return 2;
}

FAIL? O Bob é um cara preguiçoso, então ele escreveu um código que sempre retorna dois. Isso faz o teste passar, mas não era isso que a Alice tinha em mente!

Surpreendentemente, essa é a vantagem do ping-pong. Suponha que esse teste fosse o único teste que o código tinha. Agora digamos que alguém, anos depois, foi refatorar o código, mas fez uma bobagem no processo e agora a função que incrementa um número está retornando sempre 2. Nesse caso, o teste não vai detectar o erro!

A conclusão é que o teste inicial não era robusto o suficiente. Pra melhorar isso, Alice escreve um segundo teste:

void teste2() {
  assertEquals(3, increment(2));
}

Agora o código original do Bob não funciona, e ele precisa refatorar pra criar um código que passe os dois testes:

int increment(int value) {
  if (value == 1)
    return 2;
  else
    return 3;
}

E agora, FAIL? Não há dúvidas de que o conjunto com dois testes é mais robusto que apenas o primeiro teste, mas esse processo não parece prático. Afinal, os dois poderiam ficar no ping-pong até exaurir todos os valores do int, o que levaria um bocado de tempo.

Mas isso não acontece! Como sabemos, o Bob é preguiçoso. Na verdade, ele é tão preguiçoso, que atingiu o nível supremo da preguiça: a meta-preguiça. O Bob sabe que se ele continuar nesse ping-pong, ele vai ficar trabalhando até depois das seis, e ele quer ir pra casa ver a novela. Se a Alice escrever testes o suficiente, ela vai acabar forçando o Bob a escrever o código correto, porque é o código mais simples que resolve o problema.

void teste3() {
  assertEquals(4, increment(3));
}


int increment(int value) {
  return value + 1;
}

Agora sim! O resultado final é duplamente bom, nós temos um conjunto de testes robustos, e um código que é o mais simples possível (o que é sempre uma vantagem, esse código é o mais fácil de entender, tem o menor custo de manutenção, etc.)

Esse método me fascinou por dois motivos. Primeiro, ele é uma aplicação da Navalha de Occam em software: você parte de uma série de observações e deduz a teoria mais simples que modela o sistema. Segundo, o método é um indicativo de que é possível fazer um conjunto de testes que define a operação em questão.

Juntando as duas observações, a pergunta natural que faz é: pra que eu preciso do Bob? Eu poderia construir uma máquina que, dado um conjunto de testes, encontre o programa mais simples que os satisfaçam. Se a máquina conseguir jogar o ping-pong de maneira ótima, então acabamos de inventar o Single-Person Pair Programming!

Antes de tentar resolver esse problema, precisamos escolher alguma definição para "programa mais simples". Por exemplo, vamos escolher que o programa mais simples é o menor programa que resolve o problema. Uma maneira de achar esse programa é fazer um brute force: basta testar todos os programas possíveis!

Isso é fácil de visualizar em assembly. O conjunto de opcodes do processador é limitado, então a quantidade de programas em assembly com um único opcode é finito. Eu testo todos eles pra ver se algum satisfaz os testes: se algum passar, ele é a solução, senão, eu repito o procedimento com todos os programas de tamanho dois, e assim por diante. Esse algoritmo garantidamente acha o menor programa que satisfaz os testes.

Um problema teórico com essa abordagem é que ela está sujeita ao problema da parada de Turing. Eventualmente, algum desses programas que você está testando pode entrar num loop infinito e você não tem como detectar isso. Uma solução é sair pela tangente: a maioria dos problemas da vida real podem ser resolvidos com modelos computacionais mais fracos que a máquina de Turing. Em assembly, nós poderíamos proibir os saltos pra trás, o que resolve essa limitação.

Essa técnica para achar o programa mínimo se chama Superotimização, e hoje em dia há vários papers sobre o assunto. Em 2003 eu escrevi um superotimizador para assembly Z80, então foi fácil adaptá-lo para fazer Single-person Pair Programming.

Single-person Pair Programming escrito em C

Vamos testar. Se eu tenho um único teste, 1->2, o programa acha três soluções mínimas, sendo uma delas ADD A,A. É claro, com esse único teste, ele não sabe se estamos somando um ou multiplicando por dois. Colocando dois testes, 1->2 e 2->3, ele já converge para a solução única INC A.

Complicando: e se quisermos um incremento módulo 8 (ou seja, a=(a+1)%8)? Podemos definir isso com os testes 1->2, 2->3 e 7->0. Colocando essa suite no programa, temos o resultado abaixo:

INC A
AND 7

Ou seja, o Single-person Pair Programming funciona direitinho!

Bônus!

O vencedor do Ricbit Jam #1 foi o Davi Costa, parabéns! Por uma questão de logística que envolve a China eu ainda não tive como compilar os resultados, mas fiquem de olho lá no meu twitter que em breve eu farei uma página com soluções e comentários.

Tatuagens em cadeia

Uma classe de artistas que eu admiro muito são os tatuadores, e por um motivo simples: eles não podem errar. Um desenhista pode usar borracha, um arte-finalista pode cobrir o erro com tinta branca, um artista digital pode apertar control-Z, mas o tatuador não pode fazer nada disso. Um escultor, se erra, tem a opção de jogar fora o bloco de pedra e começar de novo, mas o tatuador nem essa opção tem.

Exatamente por isso, tem um tatuador que eu conheço que se recusa a tatuar nomes de namorados. Tatuagens são permanentes, mas namoros são efêmeros: imagine namorar alguém que tem uma tatuagem com o nome do ex? Nesse caso, uma solução prática é reciclar a tatuagem e namorar alguém que tenha o mesmo nome do seu ex. Não é elegante, mas funciona.

Isso leva a conclusões curiosas. Veja o meu caso, por exemplo. Se eu tatuar ILA e minha esposa tatuar RICARDO, aparentemente ela estaria levando vantagem. É muito mais fácil arrumar outro Ricardo que arrumar outra Ila. Por outro lado, eu não precisaria procurar apenas Ilas, eu poderia arranjar uma Priscila ou uma Camila, bastando adicionar mais letras na tatuagem!

Isso naturalmente leva à pergunta: qual é o máximo de namoradas que um Serial Tatuator pode ter? Por exemplo, uma pessoa poderia ir de Ana para Iana e depois Fabiana. Será que dá pra achar uma cadeia de tatuagens de tamanho quatro? Cinco? Hora de fazer uma simulação!

Antes de começar, precisamos de um corpus de nomes. O jeito mais fácil de conseguir o corpus é escrevendo um crawler para um desses sites com nomes de bebês. Uma busca rápida e eu achei o Babyhold, que tem a vantagem de separar os nomes por sexo.

Script python para fazer crawling de nomes de meninas

O script retornou mais de 7100 nomes de meninas. Agora é só fazer um outro script que calcule a máxima cadeia de nomes. Como a quantidade de nomes não é tão grande assim, um algoritmo cúbico bobo dá conta do recado:

Script python para achar cadeias máximas

O script acabou achando várias soluções de tamanho seis, mas sem dúvida a seqüência mais curiosa foi a abaixo :)

Li -> Lin -> Elin -> Elina -> Angelina -> Angelina Jolie

Bônus!

Embora o algoritmo cúbico funcione bem para 7100 nomes, certamente há como otimizá-lo. Ao invés de fazer uma solução mais rápida, dessa vez eu vou abrir para os leitores enviarem suas soluções! Clicando no link abaixo você vai para o primeiro Ricbit Jam, feito com a engine do spoj. Ganha quem enviar a solução mais rápida nos próximos quinze dias. Não tem prêmio, mas o vencedor terá seu nome divulgado no próximo post :)

Ricbit Jam #1

Não adianta tentar mandar o programa em python acima, ele não acha todas as soluções e vai dar TLE no servidor do spoj. Mas você pode usar como base pra fazer a sua solução.

Newton e os universos paralelos

Neste último Natal fomos passar o feriado no sítio. Não precisei de muito tempo pra notar que eu não funciono muito bem nesse ambiente. Além de ser alérgico a quase todos os insetos, eu tinha apenas uma pequena noção de coisas básicas de quem vive por lá (como andar a cavalo, por exemplo). Isso nem me chateia, porque em compensação eu tenho outras habilidades que o pessoal do sítio não tem, como saber usar o Google Sky Map pra identificar as estrelas no céu.

Enquanto eu descansava numa rede, eu comecei a pensar como seria um universo paralelo onde o Ricbit é um matuto que entende tudo da vida no campo. Mas o pensamento não durou muito. Que coisa batida isso, se for pra imaginar um universo paralelo, vamos imaginar um mais original!

Sempre que pensamos em universo paralelos, tendemos a imaginar um muito semelhante ao nosso, onde apenas alguns detalhes mudam. E se imaginássemos um universo tão diferente que até as leis físicas são distintas da nossa? Por exemplo, como seriam as órbitas planetárias num universo onde a Lei da Gravidade não variasse com o quadrado da distância, mas sim com alguma outra expressão qualquer?

Esse exemplo é bacana por causa da sua importância histórica. Vamos voltar para o tempo do Isaac Newton, que o Asimov considerava o maior de todos os cientistas. É inegável que o Newton era um gênio, mas o que nem todo mundo sabe é que ele era briguento, vingativo, e costumava cometer o maior pecado que um cientista pode fazer: não citar as fontes.

Isso aconteceu com a Lei da Gravidade. Naquela época ainda não existiam as listas de discussão, então os cientistas conversavam por cartas escritas à mão. Certa vez, Newton recebeu uma carta do Robert Hooke, aquele que hoje é conhecido pela lei da molas. Nessa carta, Hooke dizia que suspeitava da existência de uma força da gravidade, que seria central (dependendo apenas da distância), e provavelmente proporcional ao inverso do quadrado da distância. Na carta ele ainda dizia que não sabia como provar essa suspeita.

Hoje em dia a razão para o Hooke não saber provar é clara. Pra conseguir provar, você precisa saber Cálculo, que o Newton já tinha inventado, mas ainda não tinha contado pra ninguém. Se o Newton fosse gente boa, ele teria respondido algo do tipo "eu sei provar, chega mais e vamos resolver juntos". Ao invés disso, ele ficou na miúda, e anos depois publicou o Principia Mathematica, onde ele usava o Cálculo para mostrar que a tal força central inversamente quadrática implica em órbitas que são seções cônicas.

O Hooke, compreensivelmente, ficou puto, e foi reclamar com o editor do livro, o Halley (o cientista, não o cometa). Depois de muito bate-boca, o Halley convenceu o Newton a colocar um prefácio onde ele dizia que a lei da gravidade tinha sido sugerida informalmente pelo Hooke, mas sem demonstração. Numa carta posterior ao Hooke, Newton ainda diria "se enxerguei mais longe, foi porque estava sobre o ombro de gigantes". Não era humildade, era trollagem. Conta-se que Hooke era baixinho e corcunda.

Mas o Newton não parou por aí. Certa vez, ele ficou como responsável pela mudança de prédio da Royal Society. Entre os quadros que precisavam ser mudados, estavam os retratos de todos os membros do grupo. Por uma coincidência não-explicada, o quadro do Hooke foi o único que se perdeu no caminho. Hoje em dia, ninguém sabe como era o rosto do Hooke, esse quadro perdido era o único retrato dele.

Nada disso teria acontecido se o Hooke soubesse Cálculo. E nós, para calcularmos nossas órbitas em universos paralelos, vamos fazer exatamente as contas que o Hooke desconhecia! Se você também não sabe cálculo, pule a caixa azul e vá direto pro resultado.

Consideremos um sistema com duas massas pontuais no vácuo. As contas em coordenadas cartesianas são meio chatas, então vamos usar coordenadas polares, centradas numa das massas. Nesse tipo de conta, o normal é usar um sistema de versores r e θ que giram junto com o planeta, mas a engenharia me deixou vícios difíceis de largar, então eu vou usar exponenciais complexas. A posição do planeta é a seguinte:



Note que r e θ na verdade são r(t) e θ(t), eu vou omitir o tempo pra não poluir as equações. A aceleração da partícula é a segunda derivada:




Agrupando os termos e lembrando que j² = -1, temos:



Até aqui tudo genérico. Vamos impor agora que a força seja central. Nesse caso, a componente transversal vale zero. Note que, com uma pequena manipulação algébrica, dá pra isolar uma derivada:



Aqui temos duas soluções. A primeira é sem graça, 1/r=0 se as duas massas estiverem infinitamente distantes, aí naturalmente a força transversal é zero. O segundo caso é mais legal:



Se a derivada é zero, então a integral é uma constante. Se você lembrar que r²θ é o dobro da área de um setor circular, então o que essa fórmula diz é que a taxa de variação da área de um setor é constante, ou seja, para um dado intervalo de tempo, ele percorre sempre a mesma área. Ora, essa é a segunda lei de Kepler! Pelo que concluímos, ela funciona pra qualquer força central, não só pra gravidade.

Vamos lidar com a componente radial agora. As massas são todas constantes, então vale que F=ma. Além disso, vamos introduzir uma variável u pra facilitar as contas:




Nós podemos isolar o tempo e deixar o raio em função do ângulo, usando uma mudança de váriaveis com a regra da cadeia.





Agora é só substituir na equação original:




Pronto! Esta é a equação geral das órbitas com força central. Para conferir se está certo, vamos colocar uma força inversamente quadrática. Note que as forças precisam ser negativas, pois, na nossa orientação, forças atrativas são negativas. Aliás, como eu não estou interessado em unidades, vou escolher constantes que cancelem.




Para resolver a equação diferencial, somamos a solução particular com as homogêneas. Uma particular é fácil, u=1. A homogênea todo mundo sabe de cabeça, é cos(θ) (vezes uma constante que depende das condições de contorno). Afinal, é a mesma solução do sistema massa-mola, do oscilador LC, e assim por diante.



Ahá! Esta é equação da seção cônica em coordenadas polares. Dependendo do valor de e, a órbita pode ser circular (e=0, como Vênus, aproximadamente), elíptica (e<1, como a Terra), parabólica ou hiperbólica (e=1 ou e>1, como os cometas).

Vamos tentar outro tipo de força, por exemplo, uma inversamente cúbica. Nesse caso:




Ou seja, a órbita agora é uma espiral.

Agora que temos a equação geral, podemos colocar a força que quisermos, e analisar a órbita resultante. O problema é que muitas fórmulas geram equações que não tem solução analítica, então eu fiz um scriptzinho em python pra resolver numericamente mesmo. Abaixo o script e os resultados para várias funções:

Script em python para resolver órbitas em universos paralelos

Para uma força inversamente quadrática, a órbita é circular, como esperado pela Lei da Gravidade.

Já uma força inversamente cúbica gera uma espiral. Essa força é fraquinha demais pra manter uma órbita, e o planeta vai aos poucos se afastando.

Uma força inversamente linear demora para estabilizar, mas acaba fazendo uma órbita circular também.

E uma força constante, independente da distância? Ela também termina numa órbita circular, o que pra mim faz sentido. O planeta se move até o ponto onde a força constante é igual à centrípeta.

Agora vamos sacanear e colocar uma força senoidal só pra ver o que acontece. Ele não diverge, mas faz uma órbita muito doida. Provavelmente é um atrator estranho.

Ataque Cilônio!

No último post, nós vimos como funciona uma FPGA. Agora é hora de aprender a usá-la na prática, e o melhor jeito é fazendo um pequeno projetinho. Como exemplo de projetinho, eu pensei que poderíamos construir um Cilônio a partir do zero:

Para começar a desenvolver para FPGAs, a primeira coisa de que você precisa é, obviamente, uma FPGA. Se você for o tipo de ninja que consegue soldar SMD na mão, pode fazer sua própria placa de desenvolvimento. Eu, como sou inepto com ferro de solda, optei por comprar um kit de desenvolvimento na Digilent. O kit que escolhi foi o S3EBOARD, que tem o menor custo/benefício:

Essa placa custa 150 dólares. Se você comprar do Brasil, somando o frete e impostos, pode ficar meio salgado, mas no final vale a pena. Uma FPGA sozinha não serve pra muita coisa, a coisa só fica divertida quando você a usa pra controlar algum dispositivo. E essa placa da Digilent tem todos os dispositivos que você precisa! Ela tem RAM, conector VGA, PS/2 pra teclado, serial pra mouse, conector Ethernet, DACs pra fazer saída de som, enfim, com ela você pode fazer um computador completo.

Em especial, no cantinho da placa tem uma série de 8 LEDs. Com isso, já podemos escolher por onde vamos começar a fazer o nosso Cilônio. Já que temos LEDs enfileirados, vamos começar pelo visor!

Já temos uma placa com a FPGA, precisamos agora de um compilador para programá-la. Eu uso o Xilinx ISE Webpack, que é free (as in beer), e disponível para Windows e Linux. Compiladores de FPGA são análogos aos compiladores de software, até mesmo na idéia de compilar em etapas. Um compilador típico de C tem estágios de pré-processamento, compilação, otimização e linking. Um compilador para FPGA possui as seguintes etapas:

Síntese: Tudo começa com a sua descrição do projeto, feita em alguma linguagem de descrição de hardware. Para começar o processo, o compilador traduz essa linguagem para uma representação RTL, que é basicamente um sistema de equações booleanas. Essas equações são então simplificadas, de modo a eliminar redundâncias e deixar o circuito final mais rápido.

Circuito original, e circuito após otimização

Mapeamento tecnológico: Mesmo que o otimizador tenha chegado nas equações booleanas mínimas, elas ainda não podem ser usadas na FPGA. Nós sabemos que a FPGA é formada de blocos lógicos (os CLBs), então precisamos de um processo para mapear as equações nos CLBs. Note que a etapa de síntese não depende da arquitetura, mas na etapa de map o compilador precisa saber o modelo exato da FPGA sendo usada, já que cada FPGA tem um tipo de CLB diferente.

Mapeamento tecnológico, cada CLB tem um AND e um OR

Place and Route: Depois de feito o mapeamento tecnológico, o compilador sabe quantas CLBs ele precisa, e como preencher cada uma delas. Mas ele ainda não escolheu quais CLBs serão usadas. Apesar das CLBs serem todas iguais, se você utilizar CLBs muito distantes entre si, o tempo que o sinal leva de uma a outra pode influir na velocidade do seu circuito. Na etapa de place and route, o compilador escolhe a melhor disposição de CLBs para o seu design.

Antes e depois do place and route

Geração da bitstream: Por fim, o compilador gera uma bitstream que é usada pra programar a FPGA, usualmente através de uma interface JTAG. A partir desse ponto, sua FPGA está programada e pronta pra rodar :)

Agora precisamos escolher a linguagem que vamos usar. O Xilinx Webpack suporta VHDL e Verilog. Escolher uma das duas é como escolher vi ou emacs, existem fãs dos dois lados, mas na prática são quase equivalentes. Em geral, para quem está começando, eu recomendo não pensar muito e escolher aquela que seus amigos usam (assim você tem pra quem perguntar quando tiver dúvidas). Eu acabei escolhendo usar VHDL.

A origem da linguagem VHDL é curiosa. O departamento de defesa americano fazia muitos contratos de fabricação de chips, mas a documentação que vinha de cada fabricante era diferente. Eles então bolaram um padrão, o VHDL, que no começo era simplesmente um jeito de documentar circuitos. Em um certo ponto, notaram que a documentação era precisa o suficiente pra permitir simulação, e da simulação partiram para a síntese.

Mas vamos ao nosso projeto. A primeira parte de um design em VHDL, assim como em faríamos em software, são os imports:

O motivo de incluir essas bibliotecas é que sem elas não podemos usar bits em hardware. Bits em software são simples, eles podem ser 0 ou 1. Já em hardware, temos muito mais opções. Além do "0" (pino ligado no GND) e do "1" (pino ligado no Vcc), também temos o "Z" (pino não conectado), "H" (pino ligado no Vcc através de um pull-up), e assim por diante. Em VHDL, bits de hardware são chamados de std_logic.

Alguns estados do std_logic

Em seguida nós precisamos definir a entidade que vamos fazer. Uma entidade em VHDL é como uma interface em Java, ela define como seu código interage com o mundo. Em hardware, isso é equivalente a definir quem serão os pinos de entrada e saída do seu design. No nosso projeto, nós precisamos de duas entradas: um clock e um botão de liga-desliga; e oito saídas: uma para cada LED.

Agora vamos definir a implementação da interface, que em VHDL é o behaviour. No nosso projeto, vamos usar um clock de 50MHz, rápido demais para fazer a animação dos LEDs. Precisamos então dividir essa freqüência, pra isso vamos usar um contador que reseta a cada 5 milhões de ciclos. Cada vez que o contador resetar, nós incrementamos um estado da nossa máquina de estados, e, por fim, vamos associar cada estado a uma combinação de LEDs acesos e apagados.

Se fosse software, precisaríamos de três variáveis pra implementar esse algoritmo. Em hardware, não usamos variáveis, mas sim registradores. Uma parte curiosa do VHDL é que você não define os registradores diretamente; ao invés disso, você define os sinais e ele infere quais registradores você precisa. Como você deve imaginar, num projeto grande isso é fonte de inúmeros bugs! Felizmente, nesse projetinho não vamos ter esse problema.

Note que ao especificar um registrador, você precisa falar o tamanho dele. Nosso contador de clocks, por exemplo, vai de 0 a 5 milhões, e portanto cabe num registro de 23 bits. Vamos aproveitar e implementar esse contador. A diferença mais importante de hardware e software é que no hardware você tem paralelismo real, não é time-sharing e nem tem limite no número de cores. Em VHDL, cada unidade que roda em paralelo é um processo:

Na primeira linha de cada processo você define quem são as entradas (nesse caso, o clock e o valor anterior do contador). O primeiro if checa se aconteceu uma mudança no clock que o levou para o estado 1 (ou seja, o código dentro do if só roda em uma borda de subida). O resto é como em software, se chegar a 5M, volte a zero, senão incremente.

O processo seguinte faz o mesmo com o contador do estado atual:

O contador de estado incrementa na borda de subida, mas só quando o contador de clock é zero. Além disso, nós também zeramos o estado quando a chave SW0 está desligada (implementando assim um botão que liga e desliga).

Agora precisamos associar cada estado a uma combinação de LEDs (o que, em hardware, chamamos de demultiplexação):

Note que além de definir todos os estados possível, ainda temos um else extra. Precisamos sempre lembrar que, em hardware, bits não são apenas 0 ou 1! Se o estado cair em algum dos outros valores, como Z ou H, precisamos do else extra para cuidar dele.

Por fim, precisamos ligar o demultiplexador nos pinos de saída. Ligações simples de sinais nem precisam de um processo:

Agora o VHDL está pronto, mas ainda falta um detalhe para acabar o projeto. O VHDL cuida de tudo que vai acontecer dentro da FPGA, mas ainda precisamos cuidar do que está fora dela. Pra isso, precisamos de um constraint file, que vai indicar em quais pinos da FPGA estão ligados nossos periféricos (os LEDs, o clock, etc). Esses valores nós pegamos diretamente do manual do kit da Digilent. Nossos arquivos ficaram assim, então:

Visor cilônio em VHDL
Visor cilônio (constraint file, no formato UCF)

Com tudo pronto, só precisamos compilar e fazer o upload para a FPGA :)







Agora temos o visor pronto! Só falta terminar o resto do Cilônio, que fica como exercício para o leitor :)