Primos aleatórios

Dia desses a Alice me perguntou se era possível criar um gerador de números aleatórios que só retornasse números primos. Eu respondi que sim, mas que provavelmente ela não iria gostar da resposta:

int random_prime(int n) {
 int x;
 do {
   x = random(n);
 } while (!is_prime(x));
 return x;
}

Eu sabia que o que ela queria na verdade era uma fórmula bonitinha; então, como esperado, ela não gostou :) Mas a verdade é que esse algoritmo é bem melhor que as alternativas!

Antes de mostrar porque isso é verdade, precisamos formalizar um pouco o problema. É claro que não existem algoritmos que geram números aleatórios: se você quiser aleatoriedade real, precisa pegar alguma fonte física, como o decaimento radiativo. Assumindo então que existe uma fonte física que gera uma distribuiçao uniforme sobre algum intervalo, para criar o algoritmo que retorna números primos aleatórios, basta criar uma função bijetora que leve naturais para primos. Ou seja, uma função que, para um dado um número n, retorne o n-ésimo primo.

O problema é que não existe nenhuma fórmula fechada que calcule isso de maneira eficiente. Você pode calcular alguma constante irracional que resolva o problema, no estilo da constante de Mills, só que mais cedo ou mais tarde a precisão vai te limitar. Você pode calcular o n-ésimo primo com base em alguma outra distribuição, como a função de Möbius, mas aí você só está empurrando o problema com a barriga, porque a outra função é tão difícil de calcular quanto a original.

Uma maneira sem as desvantagens acima é usar o teorema de Wilson pra chegar na seguinte fórmula:




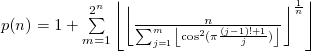
Mas mesmo essa fórmula ainda está longe do ideal, primeiro porque você vai ter que lidar com números enormes nela (pra n=10 os valores intermediários ficam tão grandes que estouram o limite do que cabe num float), segundo porque, mesmo que você use uma lib para long floats, a complexidade é O(2ⁿ), ou seja, mais lento que os programadores do Duke Nukem Forever. Se ainda assim você quiser testar, minha implementação em python é a abaixo:

Implementação em python da fórmula acima

Sendo assim, quão melhor era a implementação original por tentativa e erro? Pra avaliar isso, precisamos calcular a complexidade daquele algoritmo. Não é difícil ver que a complexidade do algoritmo como um todo é a complexidade do is_prime() multiplicado pelo valor esperado do número de iterações do loop.

Se você estiver trabalhando numa faixa pequena de primos, pode tabelar todos os primos no intervalo e fazer um is_prime() que seja O(1), mas aí também não tem necessidade da tentativa e erro, você pode indexar seu número aleatório direto na tabela. O caso legal é quando você não pode tabelar, nesse caso você pode implementar o is_prime() usando, por exemplo, o algoritmo AKS, cuja complexidade é O((log n)^10.5).

O que resta então é calcular o valor esperado do loop. Lembrando que E[x]=sum(x*p(x)), o que precisamos é calcular qual é a probabilidade de ter uma iteração, duas iterações, e assim por diante. Ora, o teorema dos números primos nos garante que a quantidade de números primos menores que n é assintoticamente igual a n/log(n), então a chance de um número ser primo, num conjunto com n elementos, é 1/log(n). Vamos chamar isso de "p" só pra ficar mais fácil, e o complemento disso é q=1-p, ou seja, a chance de um número não ser primo.

Vejamos então: pra você acertar o primo de primeira, a chance é p. Se você acertar o primo na segunda, a chance é pq. Na terceira, é pq², na quarta pq³ e assim por diante. Então o valor esperado é:

X = 1p + 2pq + 3pq² + 4pq³ + ...
X = p (1 + 2q + 3q² + 4q³ + ....)

Quem tem prática com a transformada z sabe calcular isso de cabeça, mas dá pra calcular também só com matemática elementar. Se você isolar q na soma, fica com:

X = p (1 + q(2 + 3q + 4q² + ....))

Agora você tira da cartola y=1+q+q²+q³+... e substitui:

X = p (1 + q(2 + 3q + 4q² + ....))
X = p (1 + q(y + 1 + 2q + 3q² + ....))
X = p (1 + q(y + X/p)) = p + pqy + pXq/p = p(1+qy) + Xq
X - Xq = p (1 + qy)
X (1-q) = Xp = p (1 + qy)
X = 1 + qy

Mas y é só a soma de uma PG, e isso nós sabemos que vale y=1/(1-q)=1/p. Então:

X = 1 + q/p = (p+q)/p = 1/p

Como p=1/log(n), então o valor esperado que nós queríamos é tão somente X=log n (vocês também não se impressionam quando tudo simplifica no final?)

É claro que eu não iria resistir à tentação de implementar uma simulação pra ver se o valor bate mesmo. A nossa fórmula diz que, para a faixa de 10 milhões de números, o valor esperado tem que ser da ordem de log(10⁷)=16.1. A simulação abaixo retorna 15.2, bem próximo do valor que foi predito.

Simulação monte carlo do valor esperado, em C++

No fim das contas, a complexidade do algoritmo com tentativa e erro é apenas O(log n), se você tiver um tabelão de primos. Na prática, esse é o método usado por todos que precisam de primos aleatórios: a libgcrypt usada no gpg, por exemplo, utiliza esse método na função gen_prime(), com vários truques pra tornar o teste de primalidade bem rápido.

Potências ótimas

Olhando no Google Analytics, eu descobri que alguém chegou aqui no blog procurando por "como implementar em c++ potências". Se você é essa pessoa, a resposta está abaixo. Se você não é essa pessoa, puxe uma cadeira que o papo é divertido :)


Calcular potências aproximadas em ponto flutuante é trivial, basta incluir a biblioteca <cmath> e usar a função pow, que internamente é implementada como exp(y*log(x)). Mas existem várias aplicações onde você precisa do valor exato da potência, como, por exemplo, durante a criptografia RSA. Nesses casos, uma primeira abordagem pode ser como no código abaixo:

int natural(int x, int n) {
  int result = 1;
  for (int i = 1; i <= n; i++)
    result *= x;
  return result;
}


Esse código funciona, mas existem maneiras mais espertas. Nós, que temos dez dedos, não estamos acostumados a pensar em binário. Mas se fôssemos como os golfinhos, que tem um cérebro maior que o nosso e só duas barbatanas, poderíamos visualizar o expoente em binário e fazer um código assim:

int binary(int x, int n) {
  if (n == 0) return 1;
  if (n == 1) return x;

  int half = binary(x, n/2);
  if (n & 1)
    return half*half*x;
  else
    return half*half;
}

A versão original era O(n), essa é O(log n), uma melhoria significativa. Mas a melhor notícia sobre esse algoritmo é que você não precisa implementá-lo, ele já está pronto na biblioteca padrão do C++. Basta incluir <ext/numeric> e usar a função power. A função da STL ainda recebe como argumento opcional um functor de multiplicação, então você pode implementar com ela exponenciação modular, ou até mesmo potências de matrizes (ela funciona mesmo que sua multiplicação não seja comutativa).

Por outro lado, esse algoritmo é prático, mas não é ótimo. Em alguns casos, existem maneiras mais rápidas de calcular a potência, o primeiro caso onde isso acontece é para n¹⁵. O algoritmo binário precisa de seis multiplicações para resolver o problema, mas existem soluções com apenas cinco:



A melhor maneira de descrever as multiplicações necessárias para calcular uma potência é através de uma addition chain. Uma addition chain é uma espécie de generalização da seqüência de Fibonacci: enquanto no Fibonacci o próximo elemento é a soma dos dois imediatamente precedentes, numa addition chain o próximo elemento é a soma de dois anteriores quaisquer, ou até mesmo a soma de um elemento anterior com ele mesmo (com a restrição de que a seqüência precisa ser estritamente crescente).

Pela regra de formação dá pra perceber que, ao contrário da seqüência de Fibonacci, existem inúmeras addition chains. E melhor ainda, você pode associar uma addition chain com a seqüência de expoentes gerados no cálculo de uma potência. Para o exemplo de n=15 acima, as duas addition chains correspondentes são [1 2 3 6 7 14 15] e [1 2 4 5 10 15].

Achar uma seqüência ótima para calcular potências, então, é equivalente a achar uma addition chain de tamanho mínimo terminada no número que queremos. Infelizmente, eu tenho duas más notícias: o Erdös mostrou que a addition chain ótima não cresce mais lentamente que O(log n), então assintoticamente ela não é melhor que o método binário; e pior, o cálculo da addition chain ótima é NP-Completo. Abaixo eu implementei a addition chain ótima em C++ (usando brute force, então está bem lento):

Implementação da addition chain ótima em C++

É interessante também dar uma olhada nos casos onde o binário perde. No gráfico abaixo, a linha vermelha é o método binário, a linha azul é a addition chain ótima, e a linha verde é log₂n:


Olhando o gráfico, um golfinho certamente perceberia que o desvio do método binário é proporcional à quantidade de dígitos 1 na representação binária do expoente (os picos são em 63, 127, 255, e assim por diante). A demonstração disso é bem simples e está no Seminumerical Algorithms, junto com várias heurísticas para aproximar a addition chain ótima.

Paranóia x Matemática

No último post eu falei sobre Criptografia, então agora, pra balancear, o tópico é Criptanálise. Semana passada, a polícia prendeu uma gangue que estava instalando os mini-notebooks Eee PC dentro de caixas automáticos, para roubar senhas dos usuários. O vídeo com a matéria pode ser visto abaixo:

Eu tenho certeza que um monte de gente deve ter visto a matéria e pensado "omfg nunca mais vou usar caixas automáticos kthxbye", mas na verdade, mesmo com o notebook lá dentro, não é tão fácil conseguir roubar a senha!

Se o seu banco for como o meu, você não digita a sua senha diretamente, ao invés disso, a máquina associa dois dígitos para cada botão, e você aperta os botões correspondentes à sua senha. Assim, se algum xereta estiver atrás de você olhando, ele não vai conseguir descobrir sua senha, e isso vale também se tiver um notebook dentro da máquina registrando o que você digita.

Então esse sistema é à prova de sniffers? Não! Um jeito de quebrar esse sistema é fazendo várias observações. Se o xereta te olhar uma única vez, ele não consegue descobrir sua senha, mas reduz bastante as possibilidades. Se a senha tiver quatro dígitos, uma única observação reduz de dez mil possibilidades para apenas 16. Se ele olhar uma segunda vez, pode ser que consiga informação suficiente para reduzir ainda mais o espaço, e, eventualmente, repetindo o processo, ele pode conseguir deduzir a senha.

Para conseguir reconstruir computacionalmente a senha, tudo que ele precisa fazer é resolver uma matriz de exact cover (na verdade outros métodos podem ser usados, mas eu sou preguiçoso adepto da orientação à objeto e do reuso de código pronto). Assuma n observações: para cada um dos 4 dígitos da senha há dez possibilidades, então você tem 40 linhas. Além disso, para cada observação, você precisa garantir que os quatro dígitos são consistentes, o que dá 4n colunas, e ainda mais 4 colunas extras para garantir que um único número estará associado a cada dígito da senha. No total, a matriz terá 40x(4n+4) elementos.

E quantas observações ele precisa? Isso não dá pra saber a priori, depende de como os números foram sorteados. Se a máquina repetir sempre a mesma distribuição, ele nunca vai conseguir deduzir a senha (mas também nem precisaria, pois aí ele só precisa apertar os mesmos botões que você). Por outro lado, se você tiver azar, pode ser que só duas observações sejam suficientes, como no caso abaixo:

observação 1:
senha CADA, botões A=(6 2) B=(5 8) C=(4 3) D=(1 9) E=(7 0)
observação 2:
senha CAAC, botões A=(1 2) B=(8 4) C=(6 3) D=(5 0) E=(7 9)

Nesse exemplo, dá pra ver claramente que a única senha consistente com os dados é 3216. Se o ladrão for levemente mais esperto, ele pode até perceber que não precisa fazer observações suficientes para que a senha seja única, basta que ele reduza o espaço de possibilidades para 3 ou menos (já que ele pode chutar 3 senhas antes da máquina bloquear o cartão).

Embora não seja possível calcular a priori quantas observações são necessárias, é perfeitamente possível calcular qual é o valor esperado dessa distribuição. Como eu sou preguiçoso adepto das simulações computacionais, ao invés de calcular as probabilidades na unha, eu escrevi uma simulação de Monte Carlo para calcular esse valor. O resultado é que, para uma senha de 4 dígitos, um ladrão que queira achar a senha exata precisa de 2.3 observações, enquanto que o ladrão esperto, que se contenta em reduzir pra 3 ou menos possibilidades, precisa de apenas 2.1 observações.

Código do simulador de Monte Carlo

A lição prática dessa análise é que, se você estiver desconfiado que o caixa tem um sniffer, não precisa ficar preocupado, desde que digite sua senha uma única vez. Se você precisar fazer uma outra operação, é melhor fazer em outra máquina.

A Meta-Assinatura

Como eu já disse antes, eu sou uma criatura que se empolga fácil. Ainda não tinha feito nem duas semanas que eu e o Fábio tínhamos entrado na Poli, e nós já estávamos procurando iniciação científica pra fazer. Depois de alguma procura, achamos uma legal: o Routo Terada estava procurando alunos pra estudar Criptologia.

O nosso medo inicial era que o Routo não quisesse aceitar dois alunos de primeiro ano, mas isso foi mais simples que esperávamos: "Ah, eu posso passar uma tarefa simples pra vocês. O Schneier acabou de publicar um algoritmo novo chamado Blowfish, vocês tem seis meses pra quebrar". É claro que não conseguimos quebrar o Blowfish, mas aprendemos um bocado no processo :)

Assinaturas digitais, por exemplo. O Isaac Newton, quando queria provar que algum manuscrito era dele, podia simplesmente assiná-lo com uma pena; mas o Stephen Hawking não pode fazer isso! Pra ele, o ideal são as assinaturas digitais. Para assinar digitalmente, você precisa de algum tipo de problema que seja difícil de resolver, mas que seja fácil de checar se foi resolvido (como a fatoração de números, ou o problema da sacola).

Um exemplo simples de como isso funciona me veio à mente algum tempo atrás, enquanto eu lia um livro do Hofstadter (se você não conhece o Hofstadter, tem uma entrevista dele para a rede Globo disponível online). Suponha que eu fiz uma grande descoberta e quero divulgar isso para o mundo:

O Ricardo sabe onde está o Bin Laden.

Embora tenha meu nome ali, qualquer um pode alterar e trocar o nome, então não tem como garantir que fui eu que escrevi:

O Wilerson sabe onde está o Bin Laden.

O método que eu bolei, e que na falta de nome melhor eu chamo de Meta-Assinatura, consiste em adicionar informação auto-referente à sua sentença:

O Ricardo afirma que sabe onde esta o Bin Laden, nesta sentenca com dezessete letras a, vinte e sete letras e, seis letras i, sete letras o, quatro letras u e uma letra x.

Confira que a contagem de letras está certinha. Dessa maneira, o Wilerson não pode trocar o nome na frase, pois se ele trocar, a contagem de letras vai mudar. Assim, a frase com meta-assinatura garante quem é o autor. Nesse método, contar as letras é muito simples, mas consertar a frase para o número de letras bater, é bem difícil (quer dizer, só com seis letras e algum esforço, até dá pra consertar a frase, mas se você usar o alfabeto inteiro na sua contagem, aí fica realmente complexo).

Para criar a frase com meta-assinatura, você não pode tentar procurar a solução por força bruta, porque demora demais. Uma solução mais rápida é criar uma função que conte as letras da sentença e troque os números correspondentes, e depois cruzar os dedos e torcer pro ponto fixo dessa função ser um atrator. O script em python abaixo faz isso, tomando o cuidado de detectar loops para não ficar preso:

Meta-Assinatura em python

Eu ainda não consegui assinar uma sentença usando todas as letras do alfabeto (ie, gerando um pangram), porque esse método não garante convergência. Se você conseguir, me avise :)