O olhar do macaco
RicBit e um povo da Engenharia vão até o prédio da psicologia se encontrar com um biólogo europeu. Por trás dessa aglomeração interdisciplinar, uma tese sobre a origem da humanidade, baseada na análise do olhar dos macacos. E tudo isso culminando com a conclusão do dilema: afinal, magenta é ou não uma cor? Suspense, emoção e integrais os aguardam no resto desse post!

No post anterior eu expliquei o que era o magenta, então agora é hora de ver o que é uma cor. O Kandel diz que cor é "uma experiência subjetiva relacionada à composição espectral da luz que atinge o olho", mas isso é uma simplificação. Pra ter uma experiência cromática você não precisa de luz, e nem de olho.
Certamente você já ouviu que as pessoas que levam porrada ficam "vendo estrelas". Não é só uma expressão, isso acontece de verdade. O que ocorre é que os mesmos cones da retina que convertem luz em sinais elétricos também são sensíveis a pressão. Então, se você apertar o sensor (por exemplo, com uma paulada bem dada), você vai gerar o mesmo impulso elétrico que teria sido gerado se você estivesse olhando para uma fonte luminosa. Daí, a sensação é de ver estrelas, mesmo que você esteja sem nenhuma luz, no completo escuro.
 Certo, então podemos usar os olhos mesmo sem luz. Mas nem os olhos são realmente necessários. Os sinais elétricos que vão dos cones até o córtex visual primário podem ser injetados diretamente com eletrodos: nesse caso você tem a experiência da cor sem precisar da retina. Ou então você pode injetar uma droga psicoativa como o LSD, que altera o equilíbrio químico do cérebro, causando uma experência cromática mais intensa que colocar uma camiseta branca e um monte de roupas coloridas dentro da máquina de lavar.
Certo, então podemos usar os olhos mesmo sem luz. Mas nem os olhos são realmente necessários. Os sinais elétricos que vão dos cones até o córtex visual primário podem ser injetados diretamente com eletrodos: nesse caso você tem a experiência da cor sem precisar da retina. Ou então você pode injetar uma droga psicoativa como o LSD, que altera o equilíbrio químico do cérebro, causando uma experência cromática mais intensa que colocar uma camiseta branca e um monte de roupas coloridas dentro da máquina de lavar.
Mas esses são efeitos colaterais. Na maior parte do tempo, você vai mesmo enxergar cor como sendo uma conseqüência do espectro eletromagnético. Curiosamente, tudo que eu posso afirmar é que a cor é uma conseqüência: eu não posso dizer, por exemplo, que a cor é uma função do espectro, porque ela falha em satisfazer a definição de função: você pode ter duas cores para um mesmo espectro, e dois espectros para a mesma cor. O primeiro caso pode ser visto facilmente na imagem abaixo:
 Os dois MSX produzem a sensação de duas cores diferentes, mas na verdade são o mesmo espectro (pode conferir no Photoshop)! A explicaçao é que o cérebro tem uma etapa diferencial após a captura do espectro pelos cones, então um espectro isolado pode produzir duas percepções diferentes, dependendo do que está em volta.
Os dois MSX produzem a sensação de duas cores diferentes, mas na verdade são o mesmo espectro (pode conferir no Photoshop)! A explicaçao é que o cérebro tem uma etapa diferencial após a captura do espectro pelos cones, então um espectro isolado pode produzir duas percepções diferentes, dependendo do que está em volta.
O segundo caso é mais chatinho. Eu poderia mostrar aqui dois espectros diferentes, falar que eles geram a mesma cor, e pedir pra vocês acreditarem em mim; mas resolvi fazer melhor que isso: criei um editor de espectro online! Para usar, basta desenhar um espectro com o mouse em cima da caixa bege, logo abaixo vai aparecer qual a cor que o seu olho enxergaria se estivesse vendo esse espectro. Veja como existem um monte de maneiras diferentes de fazer o amarelo. Você consegue fazer o magenta?
Source do editor de espectros online
Eu escrevi o editor usando GWT, a abscissa é o comprimento de onda (de 430nm até 650nm), a ordenada é a intensidade luminosa (em escala log), e as funções de transferência eu peguei no site do Colour and Vision Research Lab da Universidade da Califórnia em San Diego. Se você estiver lendo esse post por RSS, pode ser que o seu leitor faça sanitização de javascript e o applet não apareça; nesse caso é só ver o post original no www.ricbit.com.
Ok, agora nós sabemos que uma cor pode ser gerada por vários espectros diferentes. Por que isso acontece? A resposta é que o nosso sistema visual joga fora a maior parte da informação que entra, e para explicar os detalhes temos que entender como funcionam os cones.
Um cone é uma coisinha bem burrinha. A saída dele é binária: manda impulso elétrico ou não manda impulso elétrico; e o disparo é totalmente aleatório. Mas apesar ser aleatório, não é ruído puro, porque a probabilidade de disparo pode ser controlada através da luz que entra no sensor. Algumas freqüências fazem ele disparar com mais facilidade, e se você aumentar a intensidade da luz ele também aumenta a probabilidade.
No fim do processo, o cérebro vai interpretar esse trem de pulsos e gerar um único valor, que é uma espécie de média ponderada da luz que atingiu o cone. De outra maneira, é como se o cérebro calculasse o produto interno da função de transferência do cone com o espectro da luz incidente (lembrando que produto interno de distribuições é definido como a integral do produto das distribuições; e, de fato, no source do meu editor de espectro tem um método que faz exatamente isso). Em resumo, um cone gera um valor escalar a partir da entrada.
 Mas com um cone sozinho nós não conseguiríamos ver cores. Humanos normais possuem três deles, e na verdade é aí que entra a história do macaco. O tal biólogo europeu tinha notado que o olhar dos macacos americanos era diferente do olhar dos macacos africanos: os primeiros tinham só dois cones, enquanto que os segundos tinham três cones. Isso serve de evidência de que a espécie humana surgiu na África, e não na América (já que os macacos de lá tem o mesmo número de cones que a gente).
Mas com um cone sozinho nós não conseguiríamos ver cores. Humanos normais possuem três deles, e na verdade é aí que entra a história do macaco. O tal biólogo europeu tinha notado que o olhar dos macacos americanos era diferente do olhar dos macacos africanos: os primeiros tinham só dois cones, enquanto que os segundos tinham três cones. Isso serve de evidência de que a espécie humana surgiu na África, e não na América (já que os macacos de lá tem o mesmo número de cones que a gente).
A quantidade de cones define quão rica é sua experiência cromática. Alguns humanos nascem com apenas dois cones: são os daltônicos, que enxergam menos cores que os humanos normais. Segundo a wikipedia, entre as mulheres existe um grau significativo de tetracromia também, o que faz algum sentido pra mim (isso explicaria aquelas mulheres chatas que falam: "você não limpou direito, olha uma mancha aqui", e você olha, olha e não vê mancha alguma; vai ver ela era tetracromática e a mancha era de uma cor que você não enxerga).
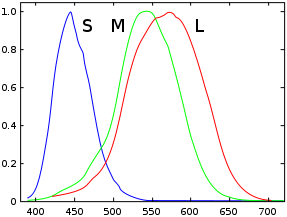
A resposta dos três cones de um humano normal é a abaixo, nós os chamamos S, M, L (baseado nos comprimentos de onda que eles cobrem, small, medium e large).
 Vamos juntar tudo agora. Um cone retorna um valor escalar, e nós temos três deles. Se podemos formar uma tripla ordenada de escalares com a saída dos cones, então na verdade eles definem um espaço vetorial de dimensão três. Uma cor, então, é simplesmente um vetor desse espaço.
Vamos juntar tudo agora. Um cone retorna um valor escalar, e nós temos três deles. Se podemos formar uma tripla ordenada de escalares com a saída dos cones, então na verdade eles definem um espaço vetorial de dimensão três. Uma cor, então, é simplesmente um vetor desse espaço.
Ora, todo espaço vetorial admite uma base. Como o espaço tem dimensão três, você pode escolher três vetores quaisquer pra formar essa base, desde que sejam linearmente independentes. O mais comum é escolher o vermelho, o verde e o azul, porque essas são as cores que você percebe quando estimulamos os nossos cones de maneira independente. Isso dá origem ao sistema RGB que todo mundo conhece.
Você pode aplicar uma transformação linear qualquer nessa base pra gerar outras, como por exemplo, o YIQ usado em transmissão NTSC, ou o YJK usado nos chips de vídeo do MSX2+. Alguns sistemas de cores são não-lineares, como o YCbCr da compressão MPEG. Um sistema não-linear muito usado por artistas é o HSV, que deforma o cubo RGB em um cilindro, onde o raio é a saturação, a altura é o brilho, e o ângulo é o tom da cor.
O sistema HSV pode ser realizado fisicamente se você tiver disponível um laser de freqüência variável e uma lâmpada de cor branca. Se você mudar a freqüência do laser, muda o tom da cor; se mudar a intensidade da lâmpada, mantendo a intensidade do laser fixa, você muda a saturação; e se mudar a intensidade dos dois ao mesmo tempo, muda o brilho. Por exemplo, eu poderia gerar um tom de rosa com um laser vermelho e com branco não muito forte. Um screenshot do editor de espectro gerando esse rosa é assim:
 E agora chegamos ao ponto crucial do problema: como você gera o magenta com esse método? A resposta é: você não gera! Não dá pra fazer o magenta assim, porque um único laser não consegue estimular o cone do vermelho e o cone do azul sem estimular junto o cone do verde.
E agora chegamos ao ponto crucial do problema: como você gera o magenta com esse método? A resposta é: você não gera! Não dá pra fazer o magenta assim, porque um único laser não consegue estimular o cone do vermelho e o cone do azul sem estimular junto o cone do verde.
Isso é evidência de que o magenta não é uma cor? Claro que não, é só uma evidência de que esse método específico de gerar cores não é capaz de percorrer todo o espaço vetorial, e algumas cores ficam de fora.
A moral da história é que pra trabalhar com cognição você precisa ter um time interdisciplinar. Se o seu time não tiver alguém de exatas pra interpretar a álgebra linear do seu problema, você corre o risco de escrever bobagens como "magenta não é uma cor".
 No próximo post, a conclusão da série do magenta, com as batalhas que a coitada da cor passou!
No próximo post, a conclusão da série do magenta, com as batalhas que a coitada da cor passou!

No post anterior eu expliquei o que era o magenta, então agora é hora de ver o que é uma cor. O Kandel diz que cor é "uma experiência subjetiva relacionada à composição espectral da luz que atinge o olho", mas isso é uma simplificação. Pra ter uma experiência cromática você não precisa de luz, e nem de olho.
 Certo, então podemos usar os olhos mesmo sem luz. Mas nem os olhos são realmente necessários. Os sinais elétricos que vão dos cones até o córtex visual primário podem ser injetados diretamente com eletrodos: nesse caso você tem a experiência da cor sem precisar da retina. Ou então você pode injetar uma droga psicoativa como o LSD, que altera o equilíbrio químico do cérebro, causando uma experência cromática mais intensa que colocar uma camiseta branca e um monte de roupas coloridas dentro da máquina de lavar.
Certo, então podemos usar os olhos mesmo sem luz. Mas nem os olhos são realmente necessários. Os sinais elétricos que vão dos cones até o córtex visual primário podem ser injetados diretamente com eletrodos: nesse caso você tem a experiência da cor sem precisar da retina. Ou então você pode injetar uma droga psicoativa como o LSD, que altera o equilíbrio químico do cérebro, causando uma experência cromática mais intensa que colocar uma camiseta branca e um monte de roupas coloridas dentro da máquina de lavar.Mas esses são efeitos colaterais. Na maior parte do tempo, você vai mesmo enxergar cor como sendo uma conseqüência do espectro eletromagnético. Curiosamente, tudo que eu posso afirmar é que a cor é uma conseqüência: eu não posso dizer, por exemplo, que a cor é uma função do espectro, porque ela falha em satisfazer a definição de função: você pode ter duas cores para um mesmo espectro, e dois espectros para a mesma cor. O primeiro caso pode ser visto facilmente na imagem abaixo:
 Os dois MSX produzem a sensação de duas cores diferentes, mas na verdade são o mesmo espectro (pode conferir no Photoshop)! A explicaçao é que o cérebro tem uma etapa diferencial após a captura do espectro pelos cones, então um espectro isolado pode produzir duas percepções diferentes, dependendo do que está em volta.
Os dois MSX produzem a sensação de duas cores diferentes, mas na verdade são o mesmo espectro (pode conferir no Photoshop)! A explicaçao é que o cérebro tem uma etapa diferencial após a captura do espectro pelos cones, então um espectro isolado pode produzir duas percepções diferentes, dependendo do que está em volta.O segundo caso é mais chatinho. Eu poderia mostrar aqui dois espectros diferentes, falar que eles geram a mesma cor, e pedir pra vocês acreditarem em mim; mas resolvi fazer melhor que isso: criei um editor de espectro online! Para usar, basta desenhar um espectro com o mouse em cima da caixa bege, logo abaixo vai aparecer qual a cor que o seu olho enxergaria se estivesse vendo esse espectro. Veja como existem um monte de maneiras diferentes de fazer o amarelo. Você consegue fazer o magenta?
Source do editor de espectros online
Eu escrevi o editor usando GWT, a abscissa é o comprimento de onda (de 430nm até 650nm), a ordenada é a intensidade luminosa (em escala log), e as funções de transferência eu peguei no site do Colour and Vision Research Lab da Universidade da Califórnia em San Diego. Se você estiver lendo esse post por RSS, pode ser que o seu leitor faça sanitização de javascript e o applet não apareça; nesse caso é só ver o post original no www.ricbit.com.
Ok, agora nós sabemos que uma cor pode ser gerada por vários espectros diferentes. Por que isso acontece? A resposta é que o nosso sistema visual joga fora a maior parte da informação que entra, e para explicar os detalhes temos que entender como funcionam os cones.
Um cone é uma coisinha bem burrinha. A saída dele é binária: manda impulso elétrico ou não manda impulso elétrico; e o disparo é totalmente aleatório. Mas apesar ser aleatório, não é ruído puro, porque a probabilidade de disparo pode ser controlada através da luz que entra no sensor. Algumas freqüências fazem ele disparar com mais facilidade, e se você aumentar a intensidade da luz ele também aumenta a probabilidade.
No fim do processo, o cérebro vai interpretar esse trem de pulsos e gerar um único valor, que é uma espécie de média ponderada da luz que atingiu o cone. De outra maneira, é como se o cérebro calculasse o produto interno da função de transferência do cone com o espectro da luz incidente (lembrando que produto interno de distribuições é definido como a integral do produto das distribuições; e, de fato, no source do meu editor de espectro tem um método que faz exatamente isso). Em resumo, um cone gera um valor escalar a partir da entrada.
 Mas com um cone sozinho nós não conseguiríamos ver cores. Humanos normais possuem três deles, e na verdade é aí que entra a história do macaco. O tal biólogo europeu tinha notado que o olhar dos macacos americanos era diferente do olhar dos macacos africanos: os primeiros tinham só dois cones, enquanto que os segundos tinham três cones. Isso serve de evidência de que a espécie humana surgiu na África, e não na América (já que os macacos de lá tem o mesmo número de cones que a gente).
Mas com um cone sozinho nós não conseguiríamos ver cores. Humanos normais possuem três deles, e na verdade é aí que entra a história do macaco. O tal biólogo europeu tinha notado que o olhar dos macacos americanos era diferente do olhar dos macacos africanos: os primeiros tinham só dois cones, enquanto que os segundos tinham três cones. Isso serve de evidência de que a espécie humana surgiu na África, e não na América (já que os macacos de lá tem o mesmo número de cones que a gente).A quantidade de cones define quão rica é sua experiência cromática. Alguns humanos nascem com apenas dois cones: são os daltônicos, que enxergam menos cores que os humanos normais. Segundo a wikipedia, entre as mulheres existe um grau significativo de tetracromia também, o que faz algum sentido pra mim (isso explicaria aquelas mulheres chatas que falam: "você não limpou direito, olha uma mancha aqui", e você olha, olha e não vê mancha alguma; vai ver ela era tetracromática e a mancha era de uma cor que você não enxerga).
A resposta dos três cones de um humano normal é a abaixo, nós os chamamos S, M, L (baseado nos comprimentos de onda que eles cobrem, small, medium e large).
 Vamos juntar tudo agora. Um cone retorna um valor escalar, e nós temos três deles. Se podemos formar uma tripla ordenada de escalares com a saída dos cones, então na verdade eles definem um espaço vetorial de dimensão três. Uma cor, então, é simplesmente um vetor desse espaço.
Vamos juntar tudo agora. Um cone retorna um valor escalar, e nós temos três deles. Se podemos formar uma tripla ordenada de escalares com a saída dos cones, então na verdade eles definem um espaço vetorial de dimensão três. Uma cor, então, é simplesmente um vetor desse espaço.Ora, todo espaço vetorial admite uma base. Como o espaço tem dimensão três, você pode escolher três vetores quaisquer pra formar essa base, desde que sejam linearmente independentes. O mais comum é escolher o vermelho, o verde e o azul, porque essas são as cores que você percebe quando estimulamos os nossos cones de maneira independente. Isso dá origem ao sistema RGB que todo mundo conhece.
Você pode aplicar uma transformação linear qualquer nessa base pra gerar outras, como por exemplo, o YIQ usado em transmissão NTSC, ou o YJK usado nos chips de vídeo do MSX2+. Alguns sistemas de cores são não-lineares, como o YCbCr da compressão MPEG. Um sistema não-linear muito usado por artistas é o HSV, que deforma o cubo RGB em um cilindro, onde o raio é a saturação, a altura é o brilho, e o ângulo é o tom da cor.
O sistema HSV pode ser realizado fisicamente se você tiver disponível um laser de freqüência variável e uma lâmpada de cor branca. Se você mudar a freqüência do laser, muda o tom da cor; se mudar a intensidade da lâmpada, mantendo a intensidade do laser fixa, você muda a saturação; e se mudar a intensidade dos dois ao mesmo tempo, muda o brilho. Por exemplo, eu poderia gerar um tom de rosa com um laser vermelho e com branco não muito forte. Um screenshot do editor de espectro gerando esse rosa é assim:
 E agora chegamos ao ponto crucial do problema: como você gera o magenta com esse método? A resposta é: você não gera! Não dá pra fazer o magenta assim, porque um único laser não consegue estimular o cone do vermelho e o cone do azul sem estimular junto o cone do verde.
E agora chegamos ao ponto crucial do problema: como você gera o magenta com esse método? A resposta é: você não gera! Não dá pra fazer o magenta assim, porque um único laser não consegue estimular o cone do vermelho e o cone do azul sem estimular junto o cone do verde.Isso é evidência de que o magenta não é uma cor? Claro que não, é só uma evidência de que esse método específico de gerar cores não é capaz de percorrer todo o espaço vetorial, e algumas cores ficam de fora.
A moral da história é que pra trabalhar com cognição você precisa ter um time interdisciplinar. Se o seu time não tiver alguém de exatas pra interpretar a álgebra linear do seu problema, você corre o risco de escrever bobagens como "magenta não é uma cor".
 No próximo post, a conclusão da série do magenta, com as batalhas que a coitada da cor passou!
No próximo post, a conclusão da série do magenta, com as batalhas que a coitada da cor passou!Marcadores: ciências cognitivas, code, cores, gwt, java, javascript, msx
