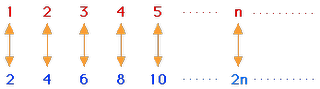
Aproximações
Ao longo da vida, encontramos aproximações a todo momento. Na escola, a gravidade é aproximadamente 10 m/s2, e a velocidade da luz é aproximadamente 3x108 m/s. Segundo a Bíblia, pi é aproximadamente três (1 Reis 7:23). Mas a minha aproximação predileta é uma que os computeiros usam a todo momento: infinito é aproximadamente oito!
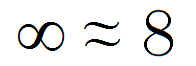 De fato, essa aproximação é o que permite aos computadores trabalhar com números negativos, através do complemento de dois. Lembrando a regra, para calcular o oposto de um número qualquer, basta inverter os bits e somar um. Vamos ver na prática como isso funciona, calculando o oposto de 5.
De fato, essa aproximação é o que permite aos computadores trabalhar com números negativos, através do complemento de dois. Lembrando a regra, para calcular o oposto de um número qualquer, basta inverter os bits e somar um. Vamos ver na prática como isso funciona, calculando o oposto de 5.
Cinco em binário é 101b, e pode ser escrito também como uma soma de potências de dois: 1+4. Para inverter os bits de 5, precisamos lembrar que há infinitos zeros na frente do 101b, então o inverso vai ter infinitas potências de dois:
Esse valor, y=~x+1, não se parece com -5. Mas as coisas ficam mais claras se você multiplicar y por dois, parcela a parcela, ...
... e depois subtrair esse valor do original:
Todos as parcelas maiores que 16 cancelam, e do lado de cá, 2y menos y é o próprio y. Então y=-5, QED. Quando calculamos complementos de dois no computador, usualmente fazemos as contas apenas em um byte, mas, no fundo, é a mesma coisa: ao invés de fazer a conta com infinitas parcelas, você aproxima o valor por apenas 8 parcelas.
 Seu professor de Cálculo 4 certamente deve ter te avisado dos horrores de manipular seqüências divergentes, que invariavelmente levam a paradoxos (como somar apenas parcelas positivas e obter um resultado negativo). No entanto, às vezes até os paradoxos têm utilidades práticas :)
Seu professor de Cálculo 4 certamente deve ter te avisado dos horrores de manipular seqüências divergentes, que invariavelmente levam a paradoxos (como somar apenas parcelas positivas e obter um resultado negativo). No entanto, às vezes até os paradoxos têm utilidades práticas :)
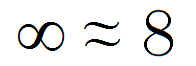 De fato, essa aproximação é o que permite aos computadores trabalhar com números negativos, através do complemento de dois. Lembrando a regra, para calcular o oposto de um número qualquer, basta inverter os bits e somar um. Vamos ver na prática como isso funciona, calculando o oposto de 5.
De fato, essa aproximação é o que permite aos computadores trabalhar com números negativos, através do complemento de dois. Lembrando a regra, para calcular o oposto de um número qualquer, basta inverter os bits e somar um. Vamos ver na prática como isso funciona, calculando o oposto de 5.Cinco em binário é 101b, e pode ser escrito também como uma soma de potências de dois: 1+4. Para inverter os bits de 5, precisamos lembrar que há infinitos zeros na frente do 101b, então o inverso vai ter infinitas potências de dois:
x = 1 + 4
~x = 2 + 8 + 16 + 32 + ...
~x+1 = 1 + 2 + 8 + 16 + 32 + ...
Esse valor, y=~x+1, não se parece com -5. Mas as coisas ficam mais claras se você multiplicar y por dois, parcela a parcela, ...
y = 1 + 2 + 8 + 16 + 32 + ...
2y = 2 + 4 + 16 + 32 + ...
... e depois subtrair esse valor do original:
2y = 2 + 4 + 16 + 32 + ...
y = 1 + 2 + 8 + 16 + 32 + ...
2y-y = -1 + 4 - 8
y = -5
Todos as parcelas maiores que 16 cancelam, e do lado de cá, 2y menos y é o próprio y. Então y=-5, QED. Quando calculamos complementos de dois no computador, usualmente fazemos as contas apenas em um byte, mas, no fundo, é a mesma coisa: ao invés de fazer a conta com infinitas parcelas, você aproxima o valor por apenas 8 parcelas.
 Seu professor de Cálculo 4 certamente deve ter te avisado dos horrores de manipular seqüências divergentes, que invariavelmente levam a paradoxos (como somar apenas parcelas positivas e obter um resultado negativo). No entanto, às vezes até os paradoxos têm utilidades práticas :)
Seu professor de Cálculo 4 certamente deve ter te avisado dos horrores de manipular seqüências divergentes, que invariavelmente levam a paradoxos (como somar apenas parcelas positivas e obter um resultado negativo). No entanto, às vezes até os paradoxos têm utilidades práticas :)
 Python foi planejada para ser legível. Os programadores mais experientes citam o
Python foi planejada para ser legível. Os programadores mais experientes citam o