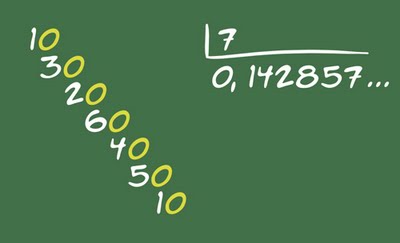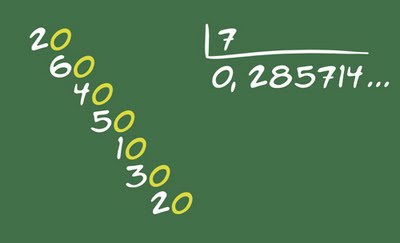Mais mágicas com calculadoras
Quando eu era criança, a mágica que eu mais gostava era aquela onde o ilusionista serra a assistente ao meio. Acho que a graça era tentar entender como ele fazia aquilo, levei um tempão para descobrir o truque. Usando uma calculadora também temos um truque parecido, mas ao invés de serrar uma assistente, vamos cortar um número em dois!
Para começar essa mágica, peça para a criança digitar o número mágico 142857 na calculadora:
Agora peça para que ela multiplique esse número por dois:
Olha só! Você cortou o número ao meio e juntou as partes ao contrário, 14-2857 virou 2857-14!
Agora peça para ela digitar novamente o número mágico e multiplicar por três:
Ahá! Novamente você cortou o número ao meio, 1-42857 virou 42857-1.
Você pode continuar a mágica a partir daqui, esse truque funciona com todos os múltiplos até 6:
Aparentemente, a parte díficil desse truque é memorizar o número mágico. Quando você está cercado de crianças barulhentas, não é fácil lembrar 142857! Mas, felizmente, você não precisa decorar o número. É só lembrar que ele é a dizíma periódica de 1/7, e você pode usar a própria calculadora para calcular a dízima:
1/7 = 0.142857142857142857...
A pergunta natural é: tem outras dízimas com essa propriedade, ou o 142857 é especial? Espantosamente, existem sim outros números. Eles tem até nome: são os números cíclicos. Para achar esses outros números, vale a pena entender porque o 1/7 funciona, e para isso é só observar o comportamento da dízima no algoritmo de divisão longa:
Você começa dividindo o número 1, e sempre que o resto é menor que 7, coloca um zero atrás e continua. Note que, quando você divide por 7, só tem sete restos possíveis: 0, 1, 2, 3, 4, 5 e 6. Se o resto for zero em algum momento, a divisão acaba e o resultado é exato. Mas se em algum momento o resto repetir, ou seja, for igual a algum resto que já apareceu antes, então você tem uma dízima.
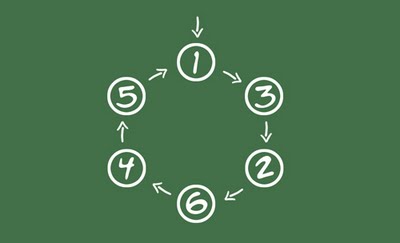
Os números cíclicos são formados por divisões de período máximo. Como você nunca pode ter um zero de resto, então no caso da dízima de 7, o maior período possível seria seis (felizmente é o caso). Você começa com o resto 1, e quando chega no 1 de novo começa a repetir, como no diagrama abaixo:
Veja como agora dá pra entender porque os números cíclicos funcionam: 142857 é a dízima de 1/7. Se a gente multiplicar 1/7 por dois, teremos 2/7, e a dízima tem que ser o dobro também. Mas se você olhar no diagrama, multiplicar por dois é a mesma coisa que começar a percorrer o diagrama a partir do 2, ao invés de começar no 1. Mas não importa de onde você começa, a seqüência será sempre a mesma, e daí o resultado vai ser uma rotação da dízima original!
Sabendo que os números cíclicos são as dízimas de período máximo, já dá pra começar a procurar propriedades desses números. Quais números, além do 7, geram dízimas de período máximo?
A primeira coisa que a gente nota é que esses números precisam ser primos. O raciocínio é relativamente simples. Vamos chamar esse número que procuramos de k, e fazer a divisão longa de 1 por k. Os restos da divisão longa formam uma recorrência, onde o primeiro termo é 1, e para os seguintes você coloca um zero no final e acha o resto da divisão por k:
R[0] = 1
R[n] = 10*R[n-1] (mod k)
Essa recorrência dá pra resolver de cabeça:
R[n] = 10n (mod k)
Para termos uma dízima de período máximo, o resto precisa ser 1 novamente quando n=k-1, ou seja:
R[k-1] = 10k-1 = 1 (mod k)
Agora, do teorema de Euler-Fermat, nós sabemos que:
10φ(k) = 1 (mod k)
Onde φ(k) é a função totiente. Ora, nós sabemos que, quando k é composto, o totiente é sempre menor que k-1, então k não pode ser composto, e portanto é primo.
Certo, então k precisa ser primo, mas qualquer primo serve? Nope. Tem alguns primos que não funcionam, como por exemplo onze. No caso do 11, é verdade que 1010 deixa resto 1, mas logo 102 já tem resto 1 também, então a dízima é muito mais curta que gostaríamos.
Na verdade, o segredo desses primos que funcionam é que... hum... ninguém sabe qual o segredo. Esse é um problema em aberto. Na verdade, a coisa é tão feia que ninguém sabe nem mesmo se esses primos são finitos ou infinitos. O melhor que podemos fazer é um script que ache os primeiros deles:
Script em python que acha os primeiros números cíclicos
Depois do sete, o primeiro primo que funciona é o 17, e o número cíclico associado é 0588235294117647. Note que esse é um caso onde o zero à esquerda faz diferença! Se a sua calculadora tiver um visor bem grande, dá pra divertir uma criança por um tempão com esse número :)
Para começar essa mágica, peça para a criança digitar o número mágico 142857 na calculadora:
Agora peça para que ela multiplique esse número por dois:
Olha só! Você cortou o número ao meio e juntou as partes ao contrário, 14-2857 virou 2857-14!
Agora peça para ela digitar novamente o número mágico e multiplicar por três:
Ahá! Novamente você cortou o número ao meio, 1-42857 virou 42857-1.
Você pode continuar a mágica a partir daqui, esse truque funciona com todos os múltiplos até 6:
142857 * 1 = 142857
142857 * 2 = 285714
142857 * 3 = 428571
142857 * 4 = 571428
142857 * 5 = 714285
142857 * 6 = 857142
Aparentemente, a parte díficil desse truque é memorizar o número mágico. Quando você está cercado de crianças barulhentas, não é fácil lembrar 142857! Mas, felizmente, você não precisa decorar o número. É só lembrar que ele é a dizíma periódica de 1/7, e você pode usar a própria calculadora para calcular a dízima:
1/7 = 0.142857142857142857...
A pergunta natural é: tem outras dízimas com essa propriedade, ou o 142857 é especial? Espantosamente, existem sim outros números. Eles tem até nome: são os números cíclicos. Para achar esses outros números, vale a pena entender porque o 1/7 funciona, e para isso é só observar o comportamento da dízima no algoritmo de divisão longa:
Você começa dividindo o número 1, e sempre que o resto é menor que 7, coloca um zero atrás e continua. Note que, quando você divide por 7, só tem sete restos possíveis: 0, 1, 2, 3, 4, 5 e 6. Se o resto for zero em algum momento, a divisão acaba e o resultado é exato. Mas se em algum momento o resto repetir, ou seja, for igual a algum resto que já apareceu antes, então você tem uma dízima.
Os números cíclicos são formados por divisões de período máximo. Como você nunca pode ter um zero de resto, então no caso da dízima de 7, o maior período possível seria seis (felizmente é o caso). Você começa com o resto 1, e quando chega no 1 de novo começa a repetir, como no diagrama abaixo:
Veja como agora dá pra entender porque os números cíclicos funcionam: 142857 é a dízima de 1/7. Se a gente multiplicar 1/7 por dois, teremos 2/7, e a dízima tem que ser o dobro também. Mas se você olhar no diagrama, multiplicar por dois é a mesma coisa que começar a percorrer o diagrama a partir do 2, ao invés de começar no 1. Mas não importa de onde você começa, a seqüência será sempre a mesma, e daí o resultado vai ser uma rotação da dízima original!
Sabendo que os números cíclicos são as dízimas de período máximo, já dá pra começar a procurar propriedades desses números. Quais números, além do 7, geram dízimas de período máximo?
A primeira coisa que a gente nota é que esses números precisam ser primos. O raciocínio é relativamente simples. Vamos chamar esse número que procuramos de k, e fazer a divisão longa de 1 por k. Os restos da divisão longa formam uma recorrência, onde o primeiro termo é 1, e para os seguintes você coloca um zero no final e acha o resto da divisão por k:
R[0] = 1
R[n] = 10*R[n-1] (mod k)
Essa recorrência dá pra resolver de cabeça:
R[n] = 10n (mod k)
Para termos uma dízima de período máximo, o resto precisa ser 1 novamente quando n=k-1, ou seja:
R[k-1] = 10k-1 = 1 (mod k)
Agora, do teorema de Euler-Fermat, nós sabemos que:
10φ(k) = 1 (mod k)
Onde φ(k) é a função totiente. Ora, nós sabemos que, quando k é composto, o totiente é sempre menor que k-1, então k não pode ser composto, e portanto é primo.
Certo, então k precisa ser primo, mas qualquer primo serve? Nope. Tem alguns primos que não funcionam, como por exemplo onze. No caso do 11, é verdade que 1010 deixa resto 1, mas logo 102 já tem resto 1 também, então a dízima é muito mais curta que gostaríamos.
Na verdade, o segredo desses primos que funcionam é que... hum... ninguém sabe qual o segredo. Esse é um problema em aberto. Na verdade, a coisa é tão feia que ninguém sabe nem mesmo se esses primos são finitos ou infinitos. O melhor que podemos fazer é um script que ache os primeiros deles:
Script em python que acha os primeiros números cíclicos
Depois do sete, o primeiro primo que funciona é o 17, e o número cíclico associado é 0588235294117647. Note que esse é um caso onde o zero à esquerda faz diferença! Se a sua calculadora tiver um visor bem grande, dá pra divertir uma criança por um tempão com esse número :)