Otimização com ábacos
Semana passada ficou pronta mais uma réplica da Máquina de Diferenças n°2 do Babbage. Essa é a segunda a ser construída a partir da especificação original, pesa 5 toneladas, e ficará em exposição no Computer History Museum de Mountain View (que eu visitei no ano passado).
 Construir a partir da especificação original é um bocado caro, e reservado só pra museus e milionários mesmo. Porém, isso não impediu um hobbysta de criar sua própria máquina de diferenças usando LEGO, o que chega a ser até mais impressionante. Pra quem quiser simular a máquina de diferenças apenas em software, pode tentar o problema CMPLS no spoj, que é exatamente isso.
Construir a partir da especificação original é um bocado caro, e reservado só pra museus e milionários mesmo. Porém, isso não impediu um hobbysta de criar sua própria máquina de diferenças usando LEGO, o que chega a ser até mais impressionante. Pra quem quiser simular a máquina de diferenças apenas em software, pode tentar o problema CMPLS no spoj, que é exatamente isso.
O que talvez não seja muito óbvio é que, apesar de usar apenas processamento mecânico, a máquina de diferenças é um computador digital (ela possui um clock, dado pela rotação de um eixo interno, e executa uma adição com carry a cada quatro rotações). Já os computadores analógicos podem ser bem mais bizarros, como o computador de sabão do post anterior.
Computadores analógicos possuem uma vantagem sobre os digitais: não estão presos aos mesmos limites computacionais. É bastante simples construir, por exemplo, um circuito, utilizando amplificadores operacionais, que resolva equações diferenciais complexas em tempo bem inferior a um computador digital (embora o processo prejudique a precisão).
Um exemplo mais curioso é o problema da ordenação de um conjunto de números. É possível demonstrar que um computador digital, usando como elemento básico de computação a comparação de dois valores, não pode ser melhor que O(n log n) (essa demostração está em qualquer livro básico de algoritmos, como o Cormen). Mas os computadores analógicos não tem essa restrição, sendo que existe até mesmo um algoritmo que resolve em O(1)!
Uma implementação simples desse algoritmo é com ábacos: primeiro você dispõe os números que você quer ordenar na base unária, como estão os números 2, 4, 1, 3, 3 na figura abaixo:
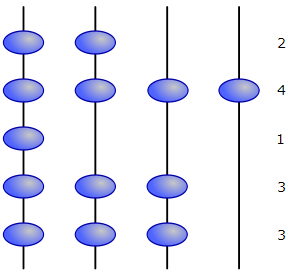
Depois, basta levantar o ábaco e deixar a gravidade fazer seu serviço:
 Impressionante, não? Os números ficam perfeitamente ordenados. Apesar de ser um truque muito simples, esse método só foi inventado em 2002. No paper original, os autores chamam o método de Bead Sort e sugerem, além da implementação com ábacos, outras implementações (com redes resistivas, autômatos celulares e matrizes de flip-flops).
Impressionante, não? Os números ficam perfeitamente ordenados. Apesar de ser um truque muito simples, esse método só foi inventado em 2002. No paper original, os autores chamam o método de Bead Sort e sugerem, além da implementação com ábacos, outras implementações (com redes resistivas, autômatos celulares e matrizes de flip-flops).
Como o Bead Sort usa operações analógicas, não dá pra analisar de verdade a complexidade computacional dele. Quando fazemos análises de big-oh, queremos saber quantos passos o algoritmo leva pra terminar, e o Bead Sort tem só um passo (levantar o ábaco), sendo que nesse aspecto ele é O(1) mesmo. Mas intuitivamente, o que queremos quando fazemos análise de complexidade é descobrir como o tempo de execução varia com o tamanho da entrada. Desse ponto de vista, a complexidade é O(sqrt(n)), se você considerar o tempo que uma bolinha leva pra ser puxada pela gravidade (no vácuo), ou então O(n), se você levar em conta que a bolinha vai atingir uma velocidade terminal devido à resistência do ar.
 Construir a partir da especificação original é um bocado caro, e reservado só pra museus e milionários mesmo. Porém, isso não impediu um hobbysta de criar sua própria máquina de diferenças usando LEGO, o que chega a ser até mais impressionante. Pra quem quiser simular a máquina de diferenças apenas em software, pode tentar o problema CMPLS no spoj, que é exatamente isso.
Construir a partir da especificação original é um bocado caro, e reservado só pra museus e milionários mesmo. Porém, isso não impediu um hobbysta de criar sua própria máquina de diferenças usando LEGO, o que chega a ser até mais impressionante. Pra quem quiser simular a máquina de diferenças apenas em software, pode tentar o problema CMPLS no spoj, que é exatamente isso.O que talvez não seja muito óbvio é que, apesar de usar apenas processamento mecânico, a máquina de diferenças é um computador digital (ela possui um clock, dado pela rotação de um eixo interno, e executa uma adição com carry a cada quatro rotações). Já os computadores analógicos podem ser bem mais bizarros, como o computador de sabão do post anterior.
Computadores analógicos possuem uma vantagem sobre os digitais: não estão presos aos mesmos limites computacionais. É bastante simples construir, por exemplo, um circuito, utilizando amplificadores operacionais, que resolva equações diferenciais complexas em tempo bem inferior a um computador digital (embora o processo prejudique a precisão).
Um exemplo mais curioso é o problema da ordenação de um conjunto de números. É possível demonstrar que um computador digital, usando como elemento básico de computação a comparação de dois valores, não pode ser melhor que O(n log n) (essa demostração está em qualquer livro básico de algoritmos, como o Cormen). Mas os computadores analógicos não tem essa restrição, sendo que existe até mesmo um algoritmo que resolve em O(1)!
Uma implementação simples desse algoritmo é com ábacos: primeiro você dispõe os números que você quer ordenar na base unária, como estão os números 2, 4, 1, 3, 3 na figura abaixo:

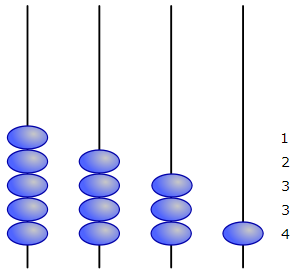
Depois, basta levantar o ábaco e deixar a gravidade fazer seu serviço:
 Impressionante, não? Os números ficam perfeitamente ordenados. Apesar de ser um truque muito simples, esse método só foi inventado em 2002. No paper original, os autores chamam o método de Bead Sort e sugerem, além da implementação com ábacos, outras implementações (com redes resistivas, autômatos celulares e matrizes de flip-flops).
Impressionante, não? Os números ficam perfeitamente ordenados. Apesar de ser um truque muito simples, esse método só foi inventado em 2002. No paper original, os autores chamam o método de Bead Sort e sugerem, além da implementação com ábacos, outras implementações (com redes resistivas, autômatos celulares e matrizes de flip-flops).Como o Bead Sort usa operações analógicas, não dá pra analisar de verdade a complexidade computacional dele. Quando fazemos análises de big-oh, queremos saber quantos passos o algoritmo leva pra terminar, e o Bead Sort tem só um passo (levantar o ábaco), sendo que nesse aspecto ele é O(1) mesmo. Mas intuitivamente, o que queremos quando fazemos análise de complexidade é descobrir como o tempo de execução varia com o tamanho da entrada. Desse ponto de vista, a complexidade é O(sqrt(n)), se você considerar o tempo que uma bolinha leva pra ser puxada pela gravidade (no vácuo), ou então O(n), se você levar em conta que a bolinha vai atingir uma velocidade terminal devido à resistência do ar.
Marcadores: complexidade, computação analógica, ordenação
